Разложение вектора в декартовом базисе
Пусть на плоскости задана д.п.с.к. X0Y.
Пусть единичный вектор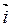 
принадлежит оси 0X.
Пусть единичный вектор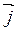 
принадлежит оси 0Y.
Очевидно, что эти векторы взаимно перпендикулярны.
 |
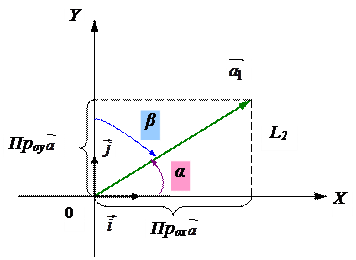Пусть Прox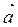 
= ax , Прoy 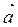=ay .
По правилу сложения двух векторов
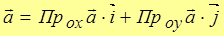или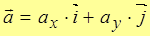 
.
Т.о., последнее равенство называется разложением вектора 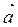в декартовом базисе пространства L2.
| Note 1 | Дома или на п/з доказать, что  .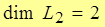
|
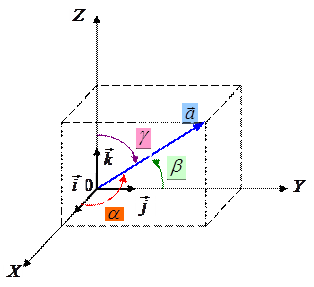
Пусть в трехмерном пространстве задана д.п.с.к. XYZ. Пусть единичный вектор 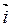принадлежит оси 0X, вектор 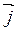– оси 0Y и единичный вектор 
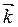принадлежит оси 0Z.
Пусть вектор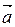 
образует углы 
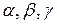с осями координат 0X, 0Y, 0Z.
Пусть Прox 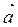= ax , Прoy 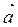=ay , Прo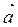z =az .
 |
По правилу сложения трех векторов
или
.
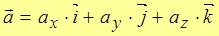Т.о., последнее равенство называется разложением вектора 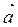в декартовом базисе пространства L3.
| Note 2 | Дома или на п/з доказать, что  .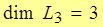
|
Пусть ax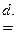 
| 
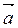|cosα, ay 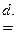| |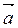cosβ , az 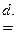| |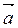cosγ.
| Note 3 | Дома или на п/з доказать, что  .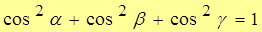
|
Пусть заданы два вектора:
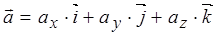и 
.
| Note 4 | Дома или на п/з доказать, что  .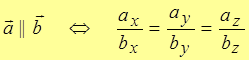
|
Дата добавления: 2015-08-20; просмотров: 895;