Преобразование координат при преобразовании базиса n-мерного линейного пространства
Пусть 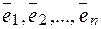 и
и 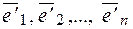 - два произвольных базиса
- два произвольных базиса 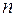 -мерного пространства R, тогда
-мерного пространства R, тогда 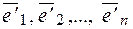 может быть разложен по базису
может быть разложен по базису 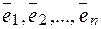 , т. е.
, т. е.
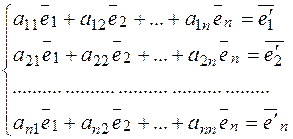 или
или 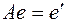 ,
, 
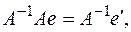
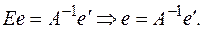 Умножим каждое уравнение системы на алгебраические дополнения
Умножим каждое уравнение системы на алгебраические дополнения 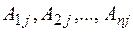 элементов j-го столбца определителя
элементов j-го столбца определителя 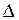 и сложим все уравнения, в результате получаем:
и сложим все уравнения, в результате получаем:
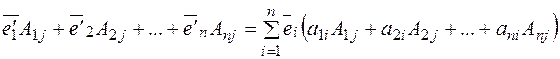 ,
, 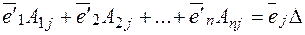 , для
, для 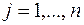 ,
,
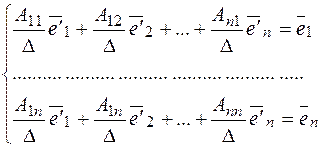 , где коэффициенты представляют матрицу равную
, где коэффициенты представляют матрицу равную 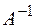 , т.е. переход от одного к другому базису осуществляется с помощью обратной матрицы
, т.е. переход от одного к другому базису осуществляется с помощью обратной матрицы 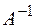 , если
, если 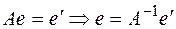 .
.
Утверждение. Если переход от одного базиса к другому осуществляется с помощью невырожденной матрицы 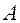 , то переход от координат произведения элемента относительно первого базиса к координатам этого элемента относительно второго базиса осуществляется с помощью матрицы
, то переход от координат произведения элемента относительно первого базиса к координатам этого элемента относительно второго базиса осуществляется с помощью матрицы 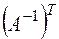 .
.
Дата добавления: 2015-08-26; просмотров: 789;
