Свойства ранга матрицы.

1Ранг произведения двух матриц не превосходит ранга сомножителей:

.

2При умножении произвольной матрицы 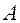слева или справа на невырожденную матрицу её 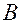ранг не изменяется. Другими словами, если 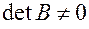, то .

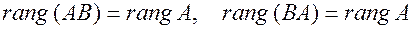Теорема: (о базисном миноре) В произвольной матрице каждый столбец является линейной комбинацией базисных столбцов, а каждая стока – линейной комбинацией базисных строк.

Следствие: Если 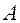квадратная матрица и 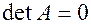, то по крайней мере один из столбцов является линейной комбинацией остальных столбцов, а так же одна из строк является линейной комбинацией остальных строк.

Теорема: (о ранге матрицы) Ранг матрицы 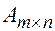равен максимальному числу линейно независимых строк и столбцов в этой матрице.

Следствие: Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов в этой матрице.