Метод элементарных преобразований матрицы.

Теорема. Элементарные преобразования не меняют ранга матрицы.

Доказательство:

1. При умножении строки на число 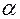базисный минор либо не измениться, либо умножится на число 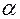. Ни один минор равный нулю при умножении на число не сделается отличным от нулю.

2. Если все миноры порядка 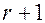равны нулю, то сложение строк не сделает их отличными от нуля, значит ранг матрицы не повысится. Он не сможет и понизиться, т.к. в противном случае, при обратном преобразовании (вычитании строк) он бы понизился.

3. при перестановке строк, минор может изменить свой знак, или замениться на минор, не больше чем знаком отличающийся от другого минора той же матрицы, или вообще не измениться.. Ясно, что порядок останется тот же.

4. Неизменность ранга при преобразовании столбцов доказывается аналогично.

Напомним, что к элементарным преобразованиям относятся:

1) умножение строки (столбца) на число отличное от нуля;

2) прибавление к одной строке (столбцу) другой строки (столбца);

3) перестановка строк (столбцов).

Элементарными преобразованиями строк заданную матрицу приводят к треугольному виду. Количество ненулевых строк (хотя бы один элемент отличен от нуля) в полученной эквивалентной матрице, дает нам ее ранг.