Обратная матрица, матричный метод решения системы. Общее решение системы.
Цель: изучить понятие обратной матрицы, ее свойства и метод вычисления. Изучить матричный метод решения СЛАУ.
Определение. Квадратная матрица 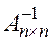 называется обратной к матрице
называется обратной к матрице 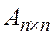 , если
, если
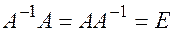 (15.1)
(15.1)
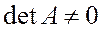 ,
, 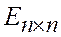 - единичная матрица.
- единичная матрица. 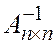 - является единственной для
- является единственной для 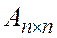 .
.
Определение.Матрица 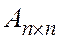 - называется неособенной (невырожденной или несингулярной) матрицей, если
- называется неособенной (невырожденной или несингулярной) матрицей, если 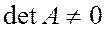 . В противном случае
. В противном случае 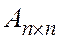 - особенная (вырожденная или сингулярная).
- особенная (вырожденная или сингулярная).
Теорема.Всякая неособенная матрица имеет обратную матрицу.
Доказательство. Рассмотрим матрицу 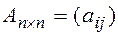 ,
, 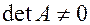 . Введем в рассмотрение матрицу
. Введем в рассмотрение матрицу 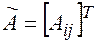 , называемую союзной матрицей элементами которой служат алгебраические дополнения матрицы
, называемую союзной матрицей элементами которой служат алгебраические дополнения матрицы 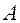 . Рассмотрим матрицу
. Рассмотрим матрицу 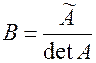 , вычислим произведение
, вычислим произведение 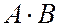 :
:
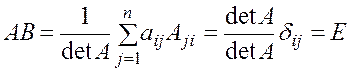 ,
,
где 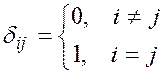 .
.
Аналогично, 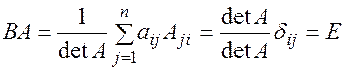 .
.
Следовательно, 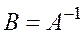 - по определению, таким образом,
- по определению, таким образом,
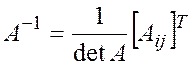 (15.2)
(15.2)
Пример.Вычислить обратную матрицу 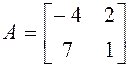
Решение.
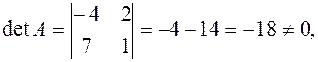
 следовательно, обратная матрица
следовательно, обратная матрица 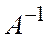 существует. Вычисляем соответствующие алгебраические дополнения
существует. Вычисляем соответствующие алгебраические дополнения
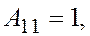
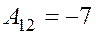 ,
, 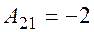 ,
, 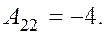
Итак, 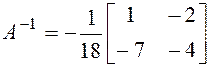 .
.
Дата добавления: 2015-08-26; просмотров: 1355;
