Фдз 13. Ортогональный и ортонормированный базисы. Ортогонализация базиса. Ортогональные матрицы.
1.В базисе 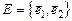 двумерного евклидова векторного пространства
двумерного евклидова векторного пространства 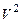 матрица
матрица 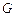 Грама имеет вид
Грама имеет вид 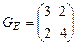 . Выяснить, будут ли векторы
. Выяснить, будут ли векторы 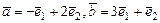 ортогональными?
ортогональными?
2. В пространстве 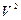 с обычным скалярным произведением в каноническом базисе
с обычным скалярным произведением в каноническом базисе 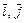
задан новый базис 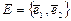 ,
, 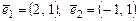 Провести ортогонализацию этого базиса. Затем, по ортогональному базису найти ортонормированный базис.
Провести ортогонализацию этого базиса. Затем, по ортогональному базису найти ортонормированный базис.
3. Возьмем 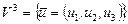 - трехмерное евклидово пространство со стандартным скалярным произведением
- трехмерное евклидово пространство со стандартным скалярным произведением 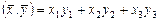 .
.
В этом пространстве задан базис 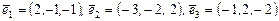 . Провести ортогонализацию этого базиса. Затем, по полученному ортогональному базису найти ортонормированный базис.
. Провести ортогонализацию этого базиса. Затем, по полученному ортогональному базису найти ортонормированный базис.
4. Дано трехмерное евклидово пространство  , у которого матрица
, у которого матрица 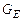 Грама в базисе
Грама в базисе  имеет вид
имеет вид 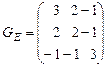 .
.  -новый базис пространства
-новый базис пространства 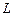 ,
,
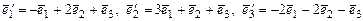 . Провести ортогонализацию базиса
. Провести ортогонализацию базиса 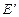 . Затем, по полученному ортогональному базису найти ортонормированный базис.
. Затем, по полученному ортогональному базису найти ортонормированный базис.
5. Дать определение ортогональной матрицы, Выяснить, какие из ниже приведенных матриц являются ортогональными.
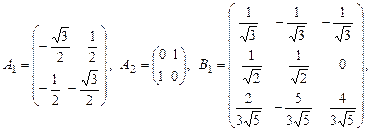
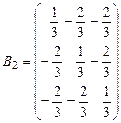 .
.
________________________________________________________________
Дата добавления: 2015-07-30; просмотров: 1225;
