Фдз 12. Евклидово пространство. Матрица Грама.

1. Дайте определение евклидова пространства.

2. Какими свойствами обладает скалярное произведение?

3. Какие из приведенных матриц могут быть матрицами Грама скалярного произведения в трехмерном евклидовом пространстве.

.

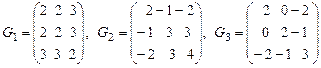4. В пространстве 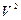с обычным скалярным произведением в каноническом базисе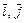

задан базис 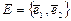. Найти матрицу Грама скалярного произведения в базисе 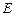, записать формулы для вычисления скалярного произведения и вычисления длины вектора в базисе 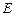, и с их помощью вычислить длины векторов 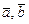, заданных в базисе 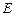, и угол между ними.

4.1. , .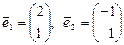

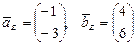4.2. , .

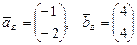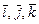5. В пространстве с обычным скалярным произведением в каноническом базисе задан базис 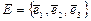. Найти матрицу Грама скалярного произведения в базисе 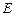, записать формулы для вычисления скалярного произведения и вычисления длины вектора в базисе 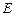, и с их помощью вычислить длины векторов 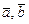, заданных в базисе 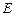и угол между ними.

, .

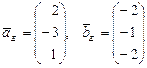6. В трехмерном евклидовом пространстве в базисе 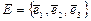матрица Грама скалярного произведения равна . 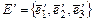- другой базис пространства 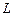, 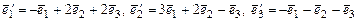. Записать формулу для скалярного произведения в базисе 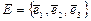. Найти матрицу Грама 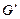в базисе 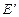двумя способами: по формуле скалярного произведения в базисе 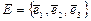и по формуле преобразования матрицы Грама при переходе от базиса 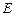к базису . _______________________________________________________________________

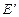Домашнее задание.

1. В пространстве с обычным скалярным произведением в каноническом базисе 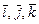задан базис 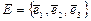. Найти матрицу Грама скалярного произведения в базисе 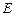и записать формулы для вычисления скалярного произведения и вычисления длины вектора в базисе 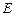, если

.

_________________________________________________________________________

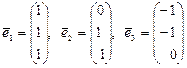Выполнить следующие пункты «своих» задач из Типового расчета: Задача 7 1)