Сопряженные и симметричные линейные операторы в евклидовом пространстве.
1. Рассмотрим двумерное евклидово пространство 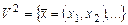 , содержащее все векторы на декартовой плоскости
, содержащее все векторы на декартовой плоскости 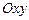 со стандартным скалярным произведением
со стандартным скалярным произведением 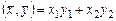 . Пусть
. Пусть  - оператор, зеркально отражающий векторы от оси
- оператор, зеркально отражающий векторы от оси 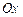 . Доказать, что
. Доказать, что 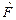 - ортогональный оператор.
- ортогональный оператор.
2. В двумерном евклидовом пространстве 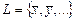 со скалярным произведением
со скалярным произведением 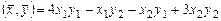 в базисе
в базисе 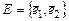 задан линейный оператор
задан линейный оператор 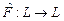 , имеющий в базисе
, имеющий в базисе 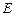 матрицу
матрицу 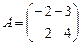 . Требуется выяснить, является ли оператор
. Требуется выяснить, является ли оператор 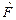 ортогональным оператором.
ортогональным оператором.
3. В рамках условий задания 2 найти матрицу 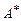 в базисе
в базисе 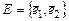 оператора
оператора 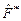 , сопряженного оператору
, сопряженного оператору 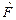 . Проверить также, что матрица
. Проверить также, что матрица 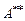 оператора
оператора 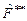 , сопряженного оператору
, сопряженного оператору 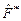 , совпадает с матрицей
, совпадает с матрицей 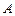 оператора
оператора 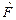 .
.
4. Найти собственный ортонормированный базис симметричного оператора 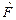 , действующего в двумерном евклидовом пространстве, если в ортонормированном базисе
, действующего в двумерном евклидовом пространстве, если в ортонормированном базисе 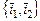 оператор
оператор 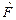 имеет матрицу
имеет матрицу 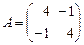 .
.
5. Найти собственный ортонормированный базис симметричного оператора 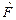 , действующего в трехмерном евклидовом пространстве, если в ортонормированном базисе
, действующего в трехмерном евклидовом пространстве, если в ортонормированном базисе 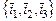 оператор
оператор 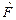 имеет матрицу
имеет матрицу 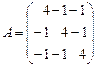 .
.
___________________________________________________________________
Дата добавления: 2015-07-30; просмотров: 913;
