Критерий базиса.

𝒜_n базис ⇔ 𝒜 линейно независима.

2 Критерий базиса.

𝒜_n базис ⇔ 𝒜_n полная система.

Доказательство: 𝒜_n линейно независима ∀𝑎̅∊V

𝒜_n+1=(𝑎₁,𝑎₂, …, 𝑎_n,𝑎̅) – линейно зависима.

𝒜_n+1 линейно зависима через базис.

n+1 ≥ n по теореме о линейной зависимости, что 𝑎_n+1 – линейно зависим ⇒

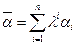
Если коэффициент при 𝑎не 0 то 𝑎выражается ⇒полная система.

Если коэффициент при 𝑎=0 то не существует 𝑎_n+1элементов ⇒противоречие.

Пусть 𝒜_n– полная.

∀𝑎̅ из V

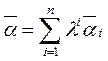
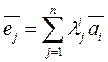
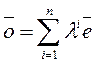
[e̅₁, e̅₂,…, e̅_n]=V

𝒜_n– полная [𝒜_n] = V

Отступление: Ранг системы векторов.

Пусть дано 𝒜_n.

Определение: Максимальное число линейно независимых векторов, называется её рангом, а векторы входящие в это число образуют ранговую подсистему.

𝒜_n– полная [𝒜_n] = V

r= rang𝒜_n= rang𝒜_r

𝒜_r⊂𝒜_n

𝒜_r- ранг подсистемы.

Справедливы следующие утверждения:

1) Любая система 𝒜_nлинейно выражается через любую свою ранговую подсистему.

2) Линейная оболочка совпадает с любой своей оболочкой подсистемы.

3) [𝒜_r] =[𝒜_n]

dim[𝒜_r] = dim[𝒜_n]=r