Элементарные преобразования системы векторов.

1) Перемена местами 2 векторов в системе.

2) Умножение какого-либо вектора системы на любое не нулевое число.

3) Прибавление к какому-либо вектору любого другого вектора.

4) Отбрасывание с противоположным(прибавление) знаком любого не нулевого вектора.

Лемма1: Каждое элементарное преобразование обратимо.

Лемма2: Две системы векторов 𝒜_nи 𝓑_kназываются эквивалентными, если одна из другой получается элементарными преобразованиями.

Если 𝒜_nэквивалентно 𝓑_k, то ранг𝒜_nравен рангу𝓑_k

dim[𝒜_m]=rang𝒜_m

Подпространство натянутые на эквивалентные системы имеют одну и ту же размерность.

𝒜_mлинейно выражается через 𝓑_n∼𝒜_m⊂[𝓑_n].

В силу свойства транзетивности линейной выражаемости, которое мы применяем в следующей ситуации:

[𝒜_m] Линейно выражается через 𝒜_mи 𝒜_mлинейно выражается через 𝓑_n⇒[𝒜_m] линейно выражается через 𝓑_n⇒[𝒜_m]⊂[𝓑_n] – по свойству транзетивности линейной выражаемости.

Если системы векторов эквивалентны:

Пусть одна система получается элементарными преобразованиями из 𝓑_n.

Система 𝒜_mполучается элементарными преобразованиями из 𝓑_n⇔𝒜_mлинейно выражается через 𝓑_n⇒[ 𝒜_m]⊂[𝓑_n].

Если 𝒜_m∼𝓑_n.⇔ [𝒜_m]=[𝓑_n]⇔𝒜_mи 𝓑_nлинейно выражаются одна через другую.

Ранг матрицы.

Берем произвольную прямоугольную матрицу

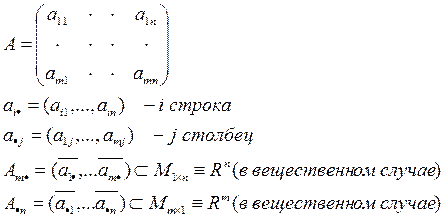
Рангом матрицы 𝒜– называется ранг системы столбцов.

rang𝒜≝rang𝒜_∙n