Векторное пространство
Теорема о пополнение
Пусть V - векторное пространство dimV=n( ∃ базис ē1 ,ē2 , … ,ēn). ∀ линейно-независимую упорядоченную систему векторов ( ƒ̅ 1 ,ƒ̅2 , … , ƒ̅n )⊂ V можно дополнить до некоторого базиса пространства V. В частности ∀ не нулевой вектор V можно включить в некоторый базис.
Если s=n, то это уже базис.
Если s>n быть не может, потому что в ∀ системе векторов больше, чем в базисе – она линейно зависима.
Если s<n :
(1) ƒ̅ 1, ƒ̅2, … , ƒ̅s, ē1, ē2 , … ,ēn – (n+s) векторов. Отбросим все векторы, которые выражаются через предыдущие. Так как Fs линейно независима, то она остается, по критерию линейно независимости.
(2) ƒ̅ 1, ƒ̅2, … , ƒ̅s, ē𝑖1, ē𝑖2 , … ,ē𝑖𝑛 составим произвольную линейную комбинацию
α1ƒ̅ 1, α2 ƒ̅2, … , αs ƒ̅s, β1ē𝑖1, β2ē𝑖2 , … ,βk ē𝑖n
βn с максимальным n, βn≠0 ⇒ ē𝑖n выражается через предыдущий ⇒ βn=0
α1ƒ̅ 1+ αs ƒ̅s=ō ⇒ α1,α2,… ,αs=0
Значит, наша система 2 линейно независима.
2 – полная система, так как ∀ вектор пространства V линейно выражается через систему 1, через 2в силу транзетивности: линейный вектор пространства V выражается через систему 2.
Следствия:
Если есть подпространство пространства, то размерность подпространства не превосходит размерность пространства: L⊂V ⇒ dimL≤dimV
dimL=dimV ⇒ L=V
Базис любого подпространства можно включить в некоторый базис объемлющего пространства.
Сумма подпространств.
Сумма подпространств – это такое множество, которое состоит из элементов одного и другого подпространств
Теорема. Размерность суммы.
Пусть U и W –конечномерные подпространства V.
dim(U+W) = dimU + dimW - dimU∩W
k = dimU p=dimW m = dimU∩W
U∩W⊂U ⇒ m ≤ k
U∩W⊂W ⇒ m ≤ p
В пересечение подпространств выбираем какой либо базис
ē1, ē2 , … ,ēm( базис U∩W) a̅1, …, a̅k-m-базис в U
ē1, ē2 , … ,ēm( базис U∩W) b̅1,…,b̅̅p-m базис в W
z = u + w u∊U,w∊W
u+w=[ ē1, ē2 , … ,ēm, a̅1, …, a̅k-m, b̅1,…,b̅̅p-m] – линейная оболочка.
Любой вектор суммы принадлежит линейной оболочке.
Осталось проверить линейную независимость.
Равенство нулю возможно только в тривиальном случае.
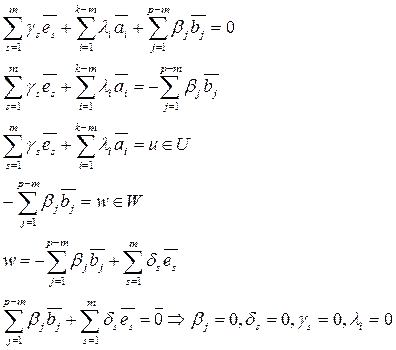
Дата добавления: 2015-07-24; просмотров: 1153;
