Параболического типа
А)Парабола
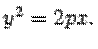
В) Пара вещественных параллельных прямых
y 2 − a2 = 0
С) Пара мнимых параллельных прямых
y2 + a2 = 0
D) Пара совпадающих прямых
y 2 = 0
Основные моменты доказательства теорем:
Коэффициенты при произведении xy либо равны 0 либо нет.
В каждой группе выделяется полный квадрат если это возможно.
Тогда уравнение будет приведено либо к 1 либо к 2 типу.
Если это невозможно, тогда один из коэффициентов при квадрате равен 0. А другой обязательно не 0 и получаем уравнение 3 типа.
А когда коэффициент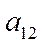 
не 0 переводим к предыдущему с помощью поворота осей.
Алгебраические поверхности 2 порядка в трехмерном Евклидовом пространстве
a11x2 + a22y2 + a33z2 + 2a12xy + 2a13xz + 2a23yz + 2a10x + 2a20y + 2a30z + a00 = 0, где коэффициенты a11, a22, a33, a12, a13, a23, a10, a20, a30, a00 − действительные числа, причем a11, a22, a33, a12, a13, a23 не равны нулю одновременно.
Особые поверхности 2 порядка:
Дата добавления: 2015-07-24; просмотров: 628;