Эксцентриситет

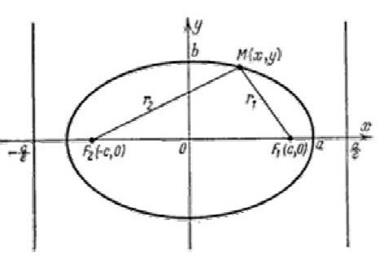
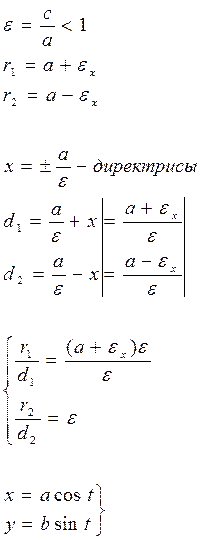параметрическое уравнение эллипса

заменим, и получим каноническое уравнение эллипса

Гипербола

Называется геометрическое место точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух фиксированных точек этой плоскости (называемых фокусами) есть величина постоянная, она меньше расстояний между фокусами.

Г - гипербола

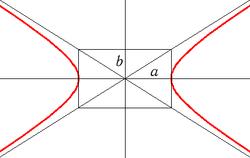
Гипербола, её полуоси и асимптоты

• Осью гиперболы называется прямая, соединяющая её фокусы.
• Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы .
• Расстояние от начала координат до одной из вершин гиперболы называется большой или вещественной полуосью гиперболы .
• Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы .
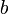• Отношение фокусного расстояния к большой полуоси гиперболы называется эксцентриситетом: 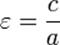. Эксцентриситет гиперболы всегда больше единицы.
• Расстояние от фокуса до гиперболы вдоль прямой, параллельной оси ординат называется фокальным параметром ..

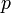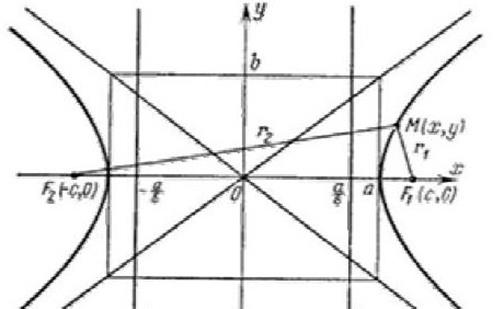
M(x, y) r₁ r₂ x F₁ a F₂

По определению ïr₁ – r₂ï= 2a. F₁, F₂ – фокусы гиперболы. F₁F₂ = 2c. Выберем на гиперболе произвольную точку М(х, у).

Тогда:

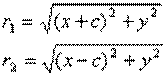
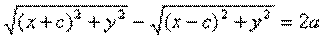
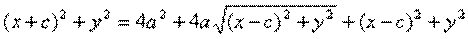
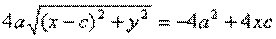
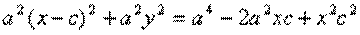
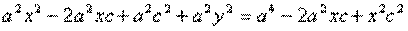
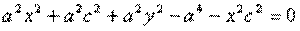
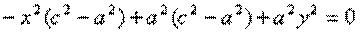
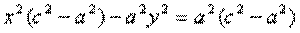
обозначим с² – а² = b² (геометрически эта величина – меньшая полуось) =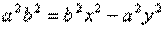

Получили каноническое уравнение гиперболы. Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которых

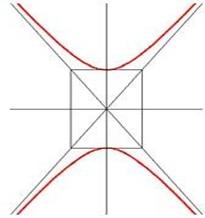
Сопряженная гипербола

Парабола

Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

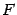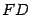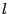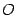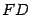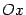Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса опустим перпендикуляр на директрису . Начало координат расположим на середине отрезка , ось направим вдоль отрезка 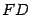так, чтобы ее направление совпадало с направлением вектора 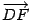. Ось Oy проведем перпендикулярно оси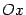

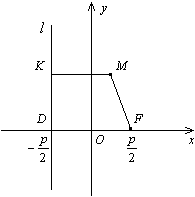
Пусть расстояние между фокусом 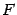и директрисой 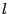параболы равно p. Тогда в выбранной системе координат парабола имеет уравнение

(*)

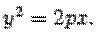
Доказательство. В выбранной системе координат фокусом параболы служит точка 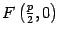, а директриса имеет уравнение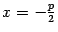

Пусть 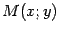-- текущая точка параболы. Тогда по формуле для плоского случая находим

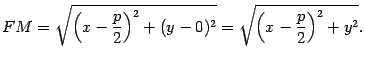
Расстоянием от точки 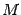до директрисы 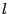служит длина перпендикуляра 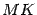, опущенного на директрису из точки 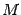. Из рисунка 12.15 очевидно, что 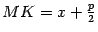. Тогда по определению параболы 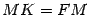, то есть

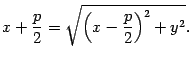
Возведем обе части последнего уравнения в квадрат:

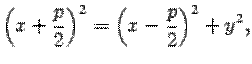
откуда

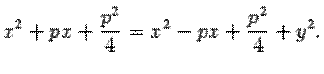
После приведения подобных членов получим уравнение (*).

Уравнение (*) называется каноническим уравнением параболы.

Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью .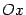

Доказательство. Проводится так же, как и предыдущее доказательство

Точка пересечения оси симметрии с параболой называется вершиной параболы.

Если переобозначить переменные 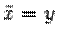, , 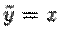то уравнение (*) можно записать в виде

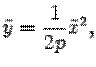
который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований

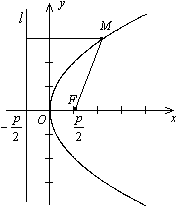
Уравнение директрисы 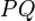: 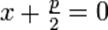, фокус — 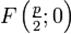, таким образом начало координат 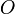— середина отрезка 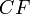. По определению параболы для любой точки 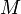, лежащей на ней выполняется равенство 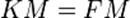. 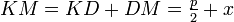и 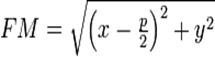, тогда равенство приобретает вид:

.

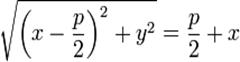После возведения в квадрат и некоторых преобразований получается равносильное уравнение .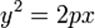

• Парабола — кривая второго порядка.
• Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.
• Пучок лучей параллельных оси, отражаясь в параболе собирается в её фокусе. Для параболы 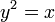фокус находится в точке (0,25; 0).
• Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
• Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
• При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

Вид кривой	Каноническое уравнение	Инварианты
Невырожденные кривые ( )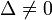
Эллипс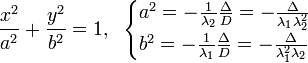
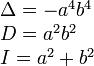
Гипербола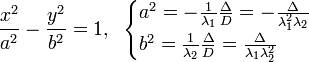
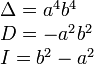
Парабола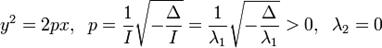
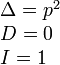
Вырожденные кривые (Δ = 0)
Точка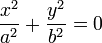
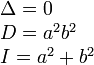
Две пересекающиеся прямые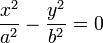
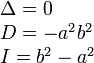
Две параллельные прямые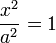
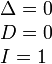
Одна прямая	x2 = 0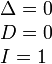

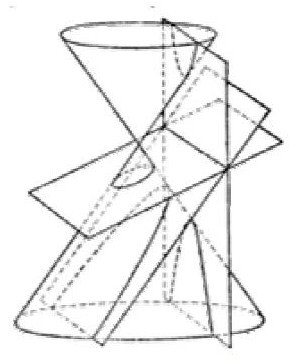
Конические сечения