Линейное свойство определителя.
Определение 2. Некоторая строка ( 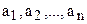 ) является линейной комбинацией строк (
) является линейной комбинацией строк ( 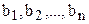 ) и (
) и ( 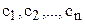 ) с коэффициентами
) с коэффициентами 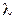 и
и 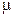 , если
, если 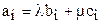 .
.
Пользуясь этим определением, перейдем к самому свойству.
Свойство 3. Если в определителе 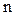 -го порядка
-го порядка 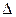 некоторая строка
некоторая строка 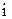 (
(  ) является линейной комбинацией двух строк (
) является линейной комбинацией двух строк ( 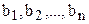 ) и (
) и ( 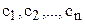 ) с коэффициентами
) с коэффициентами 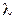 и
и 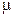 , то
, то 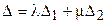 , где
, где 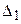 - определитель, у которого
- определитель, у которого 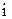 -ая строка равна (
-ая строка равна ( 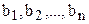 ), а все остальные - те же, что и у
), а все остальные - те же, что и у 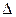 , а
, а 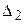 - определитель, у которого
- определитель, у которого 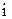 -ая строка равна (
-ая строка равна ( 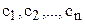 ), а все остальные - те же, что и у
), а все остальные - те же, что и у 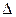 .
.
Для доказательства разложим каждый из определителей по 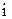 -ой строке. Очевидно, что у всех разложений миноры
-ой строке. Очевидно, что у всех разложений миноры 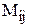 соответствующих элементов будут одинаковы. Вычислим
соответствующих элементов будут одинаковы. Вычислим 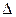 :
:
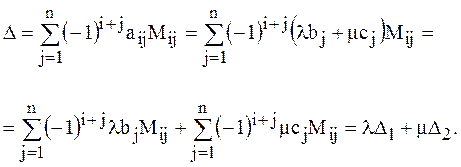
Итак, свойство доказано. Очевидно, оно справедливо и для столбцов.
Приведенные три свойства называются основными. Остальные являются их следствиями.
Свойство 4. Умножение всех элементов некоторой строки или столбца определителя на число 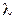 равносильно умножению определителя на число
равносильно умножению определителя на число 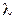 .
.
Для доказательства положим в свойстве 3  , тогда получим
, тогда получим 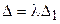 . Значит, общий множитель всех элементов некоторого ряда можно выносить за определитель.
. Значит, общий множитель всех элементов некоторого ряда можно выносить за определитель.
Свойство 5. Если все элементы некоторой строки или столбца определителя равны 0, то и сам определитель равен 0.
Для доказательства разложим определитель по нулевому ряду.
Свойство 6. Определитель с двумя равными строками или столбцами равен 0.
Действительно, переставив местами равные строки или столбцы, получим тот же определитель, но по свойству 2 его знак изменится на противоположный. Итак, с одной стороны 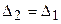 , а с другой
, а с другой  . Следовательно,
. Следовательно, 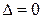 .
.
Свойство 7. Если соответствующие элементы двух строк или столбцов определителя пропорциональны, то определитель равен нулю.
Действительно, согласно свойству 4 общий множитель можно выносить за определитель, и мы получим определитель с двумя равными строками, который по свойству 6 равен нулю.
Свойство 8. Если к элементам некоторой строки или столбца определителя прибавить соответствующие элементы другой строки или столбца, умноженные на произвольный множитель 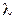 , то величина определителя не изменится.
, то величина определителя не изменится.
Доказательство. Рассмотрим определитель 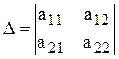 . Прибавим к элементам второй строки элементы первой с коэффициентом
. Прибавим к элементам второй строки элементы первой с коэффициентом 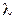 :
:
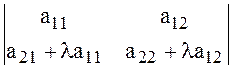 .
.
Тогда, по свойству 3 получим:
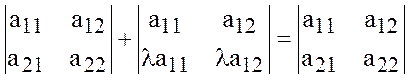 .
.
После перечисления всех свойств определителей введем еще одно определение.
Определение 3. Алгебраическим дополнением данного элемента 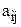 определителя
определителя 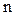 -го порядка называется число, равное
-го порядка называется число, равное 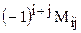 , которое обозначается
, которое обозначается 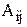 .
.
Значит, алгебраическое дополнение отличается от соответствующего минора только лишь знаком. Теперь величину определителя можно вычислить с помощью формул:
 .
.
Пользуясь свойствами, любой определитель можно вычислить не на основании основного правила, а предварительно упростив его (приводя, например, к треугольному виду).
СЛАУ.
Рассмотрим систему линейных алгебраических уравнений (СЛАУ) относительно n неизвестных x1 , x2 , ..., xn:
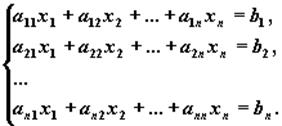
Эта система в "свернутом" виде может быть записана так:
S ni=1aij xj = bi , i=1,2, ..., n.
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме Ax=b, где
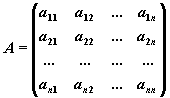 ,
, 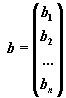 ,
, 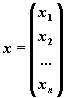 .
.
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правойчастьюсистемы. Матрица-столбец x, элементы которой - искомые неизвестные, называется решением системы.
Система линейных алгебраических уравнений, записанная в виде Ax=b, является матричным уравнением.
Если матрица системы невырождена, то у нее существует обратная матрица и тогда решение системы Ax=b дается формулой:
x=A -1 b.
Справедливо следующее утверждение (формулы Крамера).
Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x1 , x2 , ..., xn, определяемое формулами Крамера
xi =Di / D, i=1,2, ..., n,
где Di - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b.
Пример. Вычисление решения системы линейных уравнений по формулам Крамера.
Решить систему:
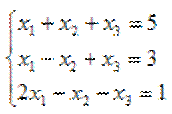
D=|A|=6
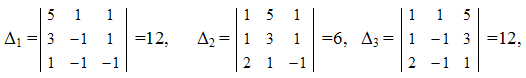
х1 = 12/6=2, х2 = 6/6=1, х3 = 12/6=2.
Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x1 , x2 , ..., xn
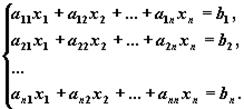
приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей
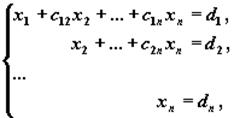
решение которой находят по рекуррентным формулам:
xn =dn , xi = di -S nk=i+1 cik xk , i=n-1, n-2, ...,1.
Матричная запись метода Гаусса.
- Прямой ход метода Гаусса: приведение расширенной матрицы системы
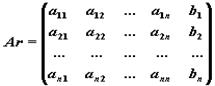
к ступенчатому виду
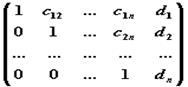
с помощью элементарных операций над строками матрицы (под элементарными операциями понимаются следующие операции:
o перестановка строк;
o умножение строки на число, отличное от нуля;
o сложение строки матрицы с другой строкой, умноженной на отличное от нуля чиcло).
- Обратный ход метода Гаусса: преобразование полученной ступенчатой матрицы к матрице, в первых n столбцах которой содержится единичная матрица
 ,
,
последний, (n+1)-й, столбец этой матрицы содержит решение системы.
Пример.
Решить систему уравнений методом Гаусса.
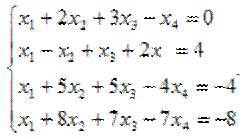
Решение:
Выписав расширенную матрицу этой системы, после ряда элементарных преобразований (проследить порядок которых рекомендуем самостоятельно), получим:
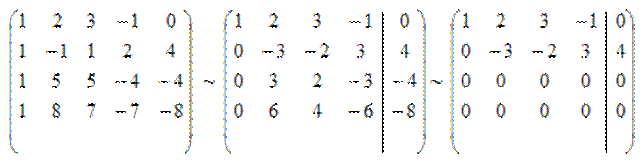
откуда
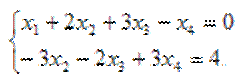
Решая последнюю систему, находим
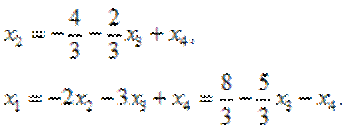
Здесь ранг расширенной матрицы равен рангу основной матрицы и равен, очевидно, двум. Система имеет бесконечно много решений, каждое из которых можно получить, придавая х3 и х4 конкретные значения.
Дата добавления: 2015-07-24; просмотров: 4776;
