Вязкостью называется свойство жидкости оказывать сопротивление сдвигу.

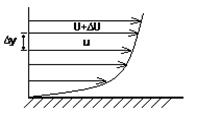Представим, что жидкость течет вдоль плоской стенки параллельными ей слоями (рис. 6.1). Вследствие тормозящего действия стенки слои жидкости будут двигаться со скоростями, значения которых возрастают по мере удаления от стенки. Ньютоном (1687 г.) впервые был установлен закон, которому подчиняется сила внутреннего трения в жидкости (сила трения между соседними слоями)

Рис.6.1 F=μS 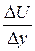, (6.1)

где F – сила трения; S – площадь слоев; μ – величина, характеризующая сопротивляемость жидкости сдвигу; DU /D y – величина, определяющая изменение скорости в направлении, перпендикулярном стенке. Величина μ называется динамической вязкостью; часто находит применение понятие кинематической вязкости

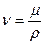, (6.2)

где ρ – плотность жидкости.

Если обе части (6.1) разделить на площадь S и перейти к пределу при ∆y→0, то получим (тем самым исключается неопределенность в понимании ∆y – расстояния между слоями и появляется возможность определять 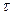в точке)

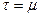
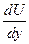, (6.3)

где τ – касательное напряжение.

Закон Ньютона вязкого трения может быть записан в виде, аналогичном (6.1)

F=μS 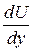. (6.4)

В системе СИ динамическая вязкость выражается в Н·с/мили Па·с; кинематическая вязкость измеряется в м²/с.

Единицей измерения кинематической вязкости в системе CGS служит стокс (сТ):

1 сТ = 1 см²/с = 10^-4 м²/с.

Для предварительных подсчетов величину кинематической вязкости воды можно принять равной 0,01 см²/с = 1·10ˉ⁶ м²/с, что отвечает температуре 20ºС. С увеличением температуры, коэффициент nводы уменьшается.

Следует отметить, что вязкость газов при нагревании возрастает, а вязкость жидкостей – уменьшается. Это свидетельствует о том, что природа внутреннего трения в газах и жидкостях различна. При нагревании газа скорость хаотического движения его молекул возрастает, их взаимодействие усиливается, увеличивается и вязкость газа. При нагревании жидкости расширяются, силы взаимного притяжения молекул уменьшаются, уменьшается и вязкость.

Задача 6.1. Определить размерности коэффициентов µ и ν.

Решение. Исходной служит зависимость (6.4), которую преобразуем к виду

µ = F/ S·d u/d u,

а размерность ν определяем с помощью ν =µ/ρ. Известные соотношения для размерностей[S] =L², [du/dy] =1/t, [F] = mL/t² и [ρ] = m/L³ подставим в формулу для µ и получим [µ] = mL/t, а также[ν] = L²/t.