Преобразование координат
Параллельный перенос:
Пусть на плоскости заданы две декартовы прямоугольные системы координат: 
("старая") и 
("новая"), причем как оси абсцисс, так и оси ординат обеих систем параллельны и одинаково направлены
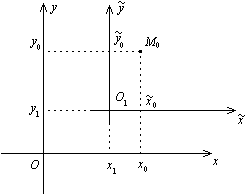
Параллельный перенос системы координат
В этом случае говорят, что одна система координат получается из другой "параллельным переносом".
Пусть начало 
"новой" системы координат имеет в "старой" системе координат координаты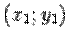 
, и пусть 
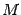-- некоторая точка плоскости. Обозначим координаты точки 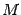в "старой" системе координат 
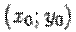, а в "новой" -- 
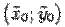. Из рис. 12.19 ясно, что 
, 
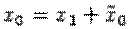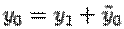. Откуда 
, 
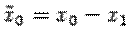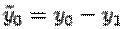. Так как точка взята произвольно, то индекс 0 в записи ее координат, как "старых", так и "новых", можно убрать. Получаем связь между "старыми" и "новыми" координатами точки при параллельном переносе осей координат:
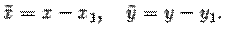
| (1) |
Выясним теперь, как связаны друг с другом уравнения одной и той же кривой в "старых" и "новых" координатах.
Пусть некоторая кривая задана уравнением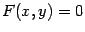 
. Тогда в системе координат 
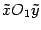, полученной параллельным переносом, с началом в точке 
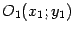уравнение кривой будет иметь вид 
.
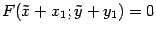Однако, для практического использования это предложение удобнее сформулировать немного по-другому.
Пусть некоторая кривая задана уравнением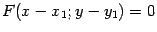 
. Тогда в системе координат 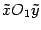, полученной параллельным переносом, с началом в точке 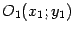уравнение кривой будет иметь вид 
.
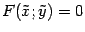Доказательство обоих предложений очевидным образом следует из формул (1) связи между старыми и новыми координатами.
Поворот: Выведем формулу преобразования координат при повороте координатных осей.Повернём оси координат на угол α относительноисходной системы координат. Координаты точки Мв системе координат x′Oy′ равны x′ и y′. Найдём еёкоординаты в системе коорднат xOy. В треугольнике CMD ∠CMD = α , OD=x′, MD=y′. Следовательно, x=OA=OB-AB=OB-CD, y=MA=AC-CM=DB+CM.Поскольку OB = x′ cos α, CD = y′ sin α, CM = y′ cos α, DB = x′ sin α, x = x′ cos α − y′ sin α,то y = x′ sin α + y′ cos α.Эти формулы выражают старые координаты (x,y) произвольной точки М через новые координаты (x′,y′) этой же точки при повороте осей на угол α. Формулы, выражающие новые координаты (x′,y′) точки М через её старые координаты (x,y), получим из следующих соображений: если новая система получена поворотом старой на угол α, то старая система получается поворотомновой на угол (-α), поэтому в равенствах можно поменять местами старые и новые координаты, заменяя одновременно α на (-α).Выполнив это преобразование, получим x′ = x cos α + y sin α, y′ = − x sin α + y cos α.При этом, например, уравнения директрис эллипса (гиперболы) и параболы принимают вид: a x′ cos α − y′ sin α = ± ; e p x′ cos α − y′ sin α = − . 2
Дата добавления: 2015-07-24; просмотров: 1654;