Эксцентриситет и директрисы гиперболы
Отношение расстояния от центра гиперболы до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и обозначается буквой е: 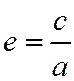 .
.
Так как для гиперболы 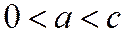 , то эксцентриситет гиперболы больше 1.
, то эксцентриситет гиперболы больше 1.
Формулы 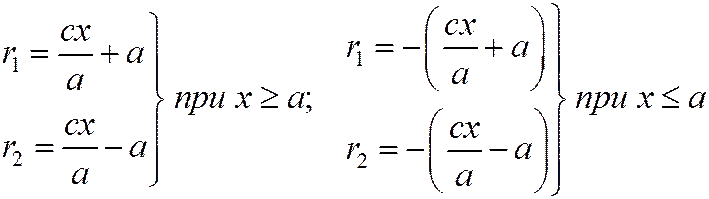 теперь можно переписать так:
теперь можно переписать так:
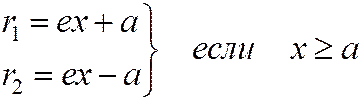 (1)
(1)
и 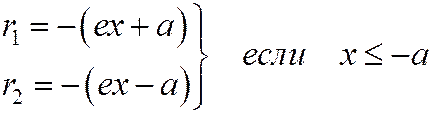 (2)
(2)
Эти четыре формулы можно объединить: 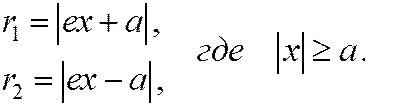 (3)
(3)
Две прямые, перпендикулярные действительной оси гиперболы и отстоящие от центра гиперболы на расстоянии 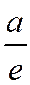 , называются директрисами гиперболы.
, называются директрисами гиперболы.
Если гипербола задана каноническим уравнением 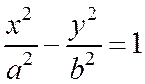 ,
,
то уравнение директрис имеют вид
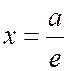 и
и  .
.
Так как эксцентриситет гиперболы больше 1, то директрисы гиперболы отстоят от ее центра на расстоянии, меньшем действительной полуоси (рис. 169). Фокус и директриса гиперболы, расположенные по одну сторону от мнимой оси, называются соответствующими друг другу. Таким образом, фокусу 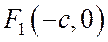 соответствует директриса
соответствует директриса 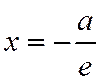 , а фокусу
, а фокусу 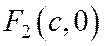 - директриса
- директриса 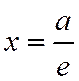 .
.
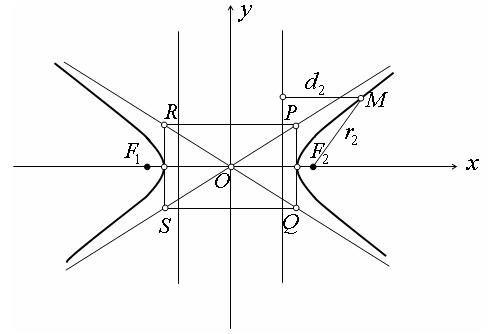
Рис. 169
Теорема. Для того, чтобы точка лежала на гиперболе, необходимо и достаточно, чтобы отношение расстояния от этой точки до фокуса гиперболы к расстоянию от той же точки до директрисы, соответствующей рассматриваемому фокусу, было равно эксцентриситету гиперболы.
Доказательство необходимости. Рассмотрим, например, фокус 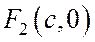 и соответствующую ему директрису
и соответствующую ему директрису  .
.
Расстояние 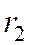 от точки М(х, у) гиперболы
от точки М(х, у) гиперболы 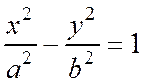 до фокуса
до фокуса  равно
равно 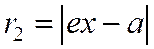 ,
,
а расстояние от той же точки М(х, у) до директрисы 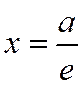 равно
равно 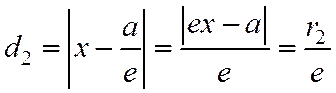 .
.
Отсюда  .
.
Аналогично доказывается, что 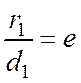 ,
,
где 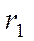 - есть расстояние от точки М(х, у) гиперболы до ее фокуса
- есть расстояние от точки М(х, у) гиперболы до ее фокуса 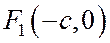 , а
, а 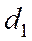 - расстояние от той же точки М до директрисы
- расстояние от той же точки М до директрисы  , соответствующей фокусу
, соответствующей фокусу 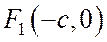 , а
, а 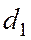 - расстояние от той же точки М до директрисы
- расстояние от той же точки М до директрисы 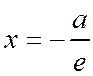 , соответствующей фокусу
, соответствующей фокусу 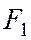 .
.
(Доказательство достаточности такое же, как и для эллипса).
Расстояние от фокуса  до директрисы
до директрисы 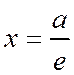 гиперболы равно
гиперболы равно  ,
,
а эксцентриситет 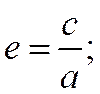
отсюда 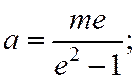
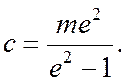
Если задана произвольная точка  прямая
прямая 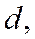 не проходящая через точку
не проходящая через точку 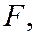 и число
и число 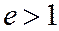 , то существует, и притом только одна гипербола, эксцентриситет которой равен е,
, то существует, и притом только одна гипербола, эксцентриситет которой равен е, 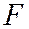 - фокус, а
- фокус, а 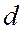 - соответствующая директриса.
- соответствующая директриса.
Центр О этой гиперболы отстоит от точки 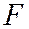 на расстоянии
на расстоянии 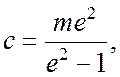
причем точки О и 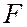 расположены по разные стороны от прямой
расположены по разные стороны от прямой 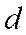 (рис.170), а большая полуось этой гиперболы равна
(рис.170), а большая полуось этой гиперболы равна 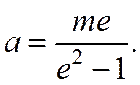
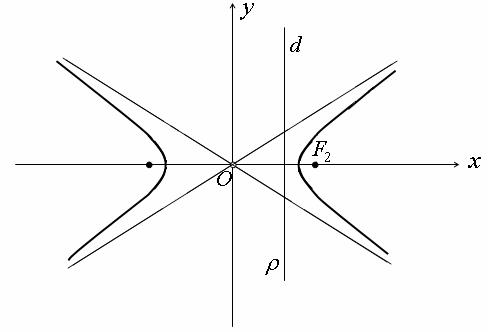
Рис. 170
Доказанная теорема и последнее утверждение позволяют дать гиперболе другое определение, эквивалентное принятому выше: гипербола есть геометрическое место точек, для каждой из которых отношение расстояния от данной точки 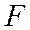 к расстоянию до данной прямой
к расстоянию до данной прямой 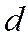 , не проходящей через точку
, не проходящей через точку 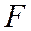 , равно данному числу
, равно данному числу 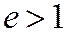 .
.
Дата добавления: 2015-08-11; просмотров: 2753;
