Исследование формы гиперболы
Так как в каноническое уравнение гиперболы координаты х и у входят во второй степени. То оси Ох и Оу являются осями симметрии гиперболы, заданной уравнением: 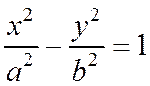 . (1)
. (1)
а начало координат – центром симметрии.
Из уравнения (1) следует, что
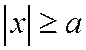 ,
,
т.е. или 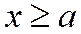 , или
, или 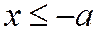 . Геометрически это означает, что между прямыми
. Геометрически это означает, что между прямыми 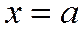 и
и  нет ни одной точки гиперболы (1).
нет ни одной точки гиперболы (1).
Ось симметрии Оу не пересекает гиперболу, заданную уравнением (1), и называется мнимой осью. Ось Ох – пересекает гиперболу (1) в двух точках:
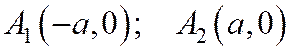 .
.
Эта ось называется действительной осью гиперболы. Точки, в которых действительная ось пересекается гиперболу, называются вершинами гиперболы.
Числа а и b в каноническом уравнении называются действительной и мнимой полуосями гиперболы.
Решая уравнение (1) относительно у, беря лишь положительное значение:  (2)
(2)
и считая 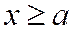 , мы получим точки гиперболы (1), лежащие в первой четверти. Из уравнения (2) следует, что у в полуинтервале
, мы получим точки гиперболы (1), лежащие в первой четверти. Из уравнения (2) следует, что у в полуинтервале 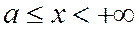 есть возрастающая функция; при этом
есть возрастающая функция; при этом
 .
.
Всякая прямая пересекает гиперболу не более чем в двух точках, так как прямая определяется уравнением первой степени, а гипербола – второй.
Рассмотрим уравнение прямой 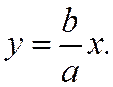 (3)
(3)
Найдем расстояние 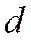 от точки М(х, у), лежащей на дуге гиперболы, определяемой уравнением (2), до прямой (3); переписывая уравнение (3) в виде
от точки М(х, у), лежащей на дуге гиперболы, определяемой уравнением (2), до прямой (3); переписывая уравнение (3) в виде 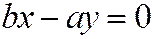 , находим:
, находим:

 Отсюда следует, то на полуинтервале
Отсюда следует, то на полуинтервале 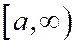 расстояние
расстояние 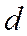 от точки М(х, у) рассматриваемой части гиперболы до прямой (3) есть убывающая функция от х и
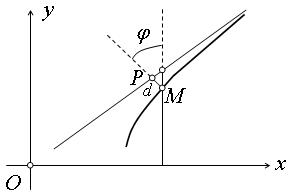
от точки М(х, у) рассматриваемой части гиперболы до прямой (3) есть убывающая функция от х и 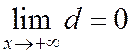 (рис. 167). Прямая, определяемая уравнением
(рис. 167). Прямая, определяемая уравнением 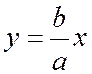 называется асимптотой гиперболы.
называется асимптотой гиперболы.
В силу того, что гипербола, заданная каноническим уравнением, симметрична относительно начала координат, расстояние от точки М(х, у), лежащей на дуге гиперболы, заданной уравнением 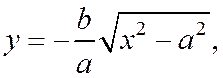 до прямой
до прямой 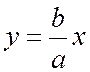 стремиться к нулю при
стремиться к нулю при 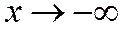 . Так как гипербола, заданная каноническим уравнением, симметрична и относительно оси Оу, то она имеет вторую асимптоту
. Так как гипербола, заданная каноническим уравнением, симметрична и относительно оси Оу, то она имеет вторую асимптоту 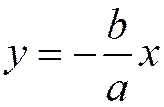 ,
,
которая обладает свойством, аналогичным свойству первой асимптоты по отношению к дугам гиперболы, расположенным во второй и четвертой четвертях.
Асимптоты гиперболы являются диагоналями прямоугольника  ,
, 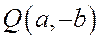 ,
,  ,
,  .
.
При одной и той же абсциссе х ординаты точки ветви гиперболы, лежащей в первой четверти, с ординатой точки асимптоты 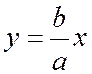 связаны неравенством:
связаны неравенством:  .
.
Отсюда и из того, что гипербола симметрична относительно осей координат, следует, что она имеет две ветви, заключенные в двух областях: одна из них ограничена отрезком 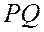 и продолжениями отрезков
и продолжениями отрезков 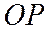 и
и 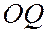 за точки
за точки 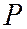 и
и 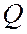 , другая симметрична этой области относительно мнимой оси гиперболы (рис 168).
, другая симметрична этой области относительно мнимой оси гиперболы (рис 168).
Рис.168 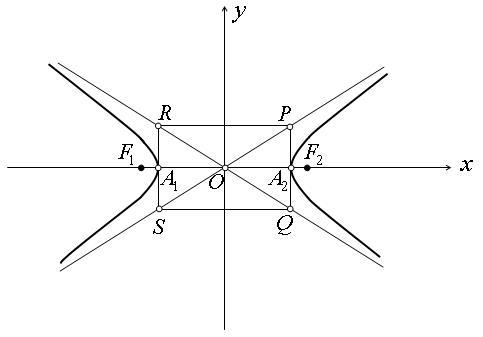
Гипербола, у которой полуоси равны, называются равносторонней. Каноническое уравнение равносторонней гиперболы имеет вид
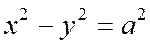
Уравнение асимптот равносторонней гиперболы таковы:
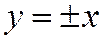 .
.
это биссектрисы углов между ее осями симметрии. Асимптоты равносторонней гиперболы взаимно перпендикулярны.
Обратно, если асимптоты гиперболы взаимно перпендикулярны, то ее полуоси равны между собой и, значит гипербола равносторонняя.
Дата добавления: 2015-08-11; просмотров: 1373;
