Оптическое свойство гиперболы.

Теорема. Касательная к гиперболе в произвольной её точке является биссектрисой внутреннего угла 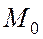треугольника 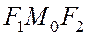, имеющего своими вершинами фокусы гиперболы и данную точку 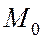.(См. рис. 173)

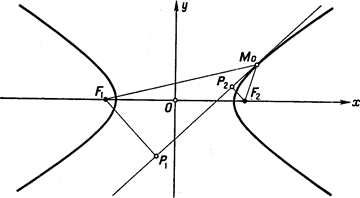Рис. 173.

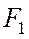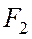Доказательство. Опустим из фокусов и перпендикуляры 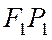и 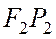на касательную. Также как и для эллипса доказывается, что 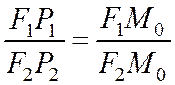. Поэтому 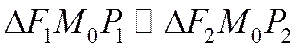и, следовательно, .

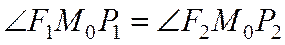Результаты подстановок координат фокусов 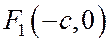и 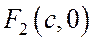в выражение 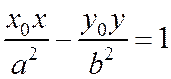- числа разных знаков, откуда следует, что фокусы гиперболы лежат по разные стороны от любой касательной к ней.

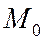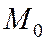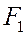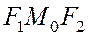Указанное геометрическое свойство позволяет построить касательную к гиперболе в произвольной точке : точку соединяем с фокусами и гиперболы и угол делим пополам; биссектриса этого угла и является касательной к гиперболе в точке .

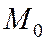Доказанной теореме можно придать оптическое истолкование, аналогичное как для эллипса. Луч света, пущенный из фокуса 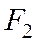, отразившись от зеркальной поверхности гиперболы, будет направлен по прямой 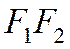(См. рис.)

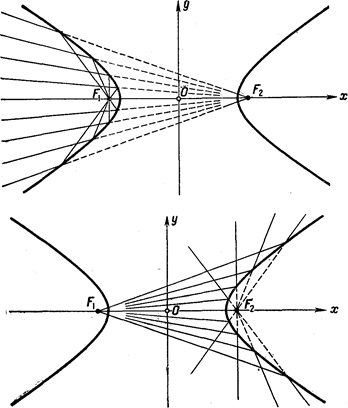Рис. 174