Основные характеристики гиперболы
1. Эксцентриситет. Величина 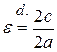 называется эксцентриситетом гиперболы.
называется эксцентриситетом гиперболы.
| Note 2 | Для гиперболы эксцентриситет 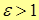 , т.к. по определению , т.к. по определению 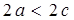 . .
|
2. Вершины: A1(-a;0) – левая действительная вершина гиперболы;
A2(a;0) – правая действительная вершина гиперболы;
B1(0;-b) – нижняя «мнимая» вершина гиперболы;
B2(0;b) – верхняя«мнимая» вершина гиперболы.
3. Длины осей: |A1A2| =2a – длина действительной оси;
|B1B2| =2b – длина «мнимой» оси.
4. Фокальные радиусы: 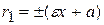 – левые;
– левые;
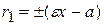 – правые.
– правые.
5. Директрисы: 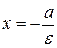 – уравнение левой директрисы;
– уравнение левой директрисы;
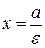 – уравнение правой директрисы.
– уравнение правой директрисы.
6. Гипербола обладает осевой и центральной симметрией.
| Note 3 | Дома или на п/з доказать, что 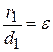 , , 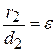 ,
где d1 – расстояние от т. М до левой директрисы,
d2 – расстояние от т. М до правой директрисы. ,
где d1 – расстояние от т. М до левой директрисы,
d2 – расстояние от т. М до правой директрисы.
|
| Note 4 | Дома или на п/з доказать, что гипербола – кривая второго порядка. |
7. Характеристический прямоугольник. Прямоугольник, проходящий через вершины гиперболы, со сторонами параллельными осям 0X и 0Y называют характеристическим.
| Note 5 | Построение гиперболы необходимо начинать с построенияхарактеристического прямоугольника и асимптот (как правило, эти построения выполняют тонкими или пунктирными линиями). |
8. Асимптоты. Прямые, проходящие через начало координат и вершины характеристического прямоугольника, называют асимптотами гиперболы.
9. Явное уравнение гиперболы. Выразив y из канонического уравнения гиперболы, получим явное уравнение 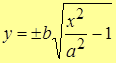 .
.
| Note 6 | Дома или на п/з доказать, что расстояние между точкой асимптоты 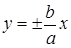 и текущей точкой гиперболы М(x;y) стремится к нулю при и текущей точкой гиперболы М(x;y) стремится к нулю при  .
Например, .
Например, 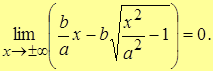
|
Дата добавления: 2015-08-20; просмотров: 1526;
