Парабола. Вывод канонического уравнения. Виды парабол
| Def. | Параболой называют геометрическое место точек плоскости, расстояние от которых до фиксированной точки, называемой фокусом, равно расстоянию до прямой, называемой директрисой. |
Пусть r – расстояние от точки параболы до фокуса;
d – расстояние от точки параболы до директрисы.
Тогда, по определению, уравнение параболы
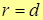 .
.
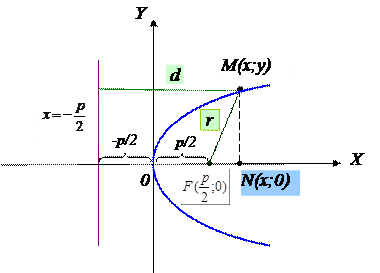
Получим уравнение параболы, расположенной в плоскости с д.п.с.к. X0Y.
Пусть фокус F принадлежит оси 0X. Директрису проведем перпендикулярно оси 0Х на расстоянии p от фокуса F. Пусть начало координат т.0 – является серединой этого расстояния.
Пусть т. M(x;y) – «текущая» точка параболы.
Пусть r – расстояние от т. M(x;y) до фокуса 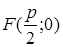 ;
;
d – расстояние от т. M(x;y) до директрисы 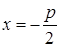 .
.
 |
По определению параболы 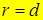 .
.
По теореме Пифагора из прямоугольного ΔF MN:
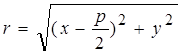 .
.
Расстояние от т. M(x;y) до директрисы 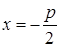
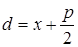 .
.
Таким образом, 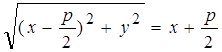 .
.
Возведя обе части в квадрат, получим
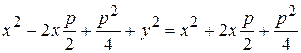 .
.
Откуда 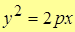 – каноническое (простейшее) уравнение параболы.
– каноническое (простейшее) уравнение параболы.
| Note 1 | Дома или на п/з доказать, что парабола – кривая второго порядка. |
Так как по определению расстояние 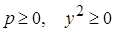 , то из уравнения параболы
, то из уравнения параболы 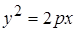 следует, что
следует, что 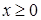 .
.
Так как в уравнении параболы ордината «текущей» точки M(x;y) y входит во второй степени, то парабола симметрична относительно оси 0Х. При этом верхнюю и нижнюю части кривой называют ветвями параболы, а начало координат т. О(0;0) – ее вершиной.
| Note 2 | Дома или на п/з обосновать различные виды парабол: |
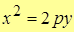
| 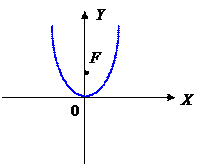
| Парабола симметричная оси 0Y, 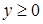 . .
| |
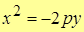
| 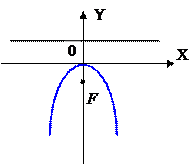
| Парабола симметричная оси 0Y, 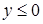 . .
| |
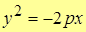
| 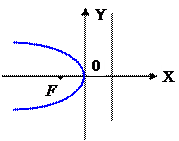
| Парабола симметричная оси 0X, 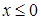 . .
|
| Note 3 | Дома или на п/з доказать, что 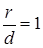 , т.е. , т.е. 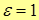 для параболы. для параболы.
|
| Note 4 | Дома или на п/з (с помощью параллельного переноса системы координат на a по оси 0Х и на b по оси 0Y) доказать, что 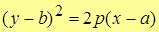 – уравнение параболы с вершиной в т.С(a;b). – уравнение параболы с вершиной в т.С(a;b).
|
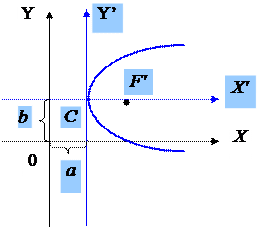 |
| Note 5 | Таким образом, основной характеристикой кривой второго порядка является ее эксцентриситет 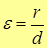 , т.е. если , т.е. если
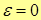 – окружность, – окружность,
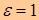 – парабола, – парабола,
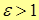 – гипербола, – гипербола,
 – эллипс. – эллипс.
|
Дата добавления: 2015-08-20; просмотров: 2156;
