Плоскость. Условие перпендикулярности и параллельности плоскостей

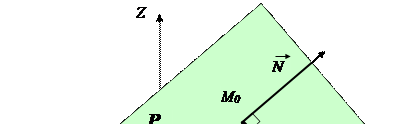
Пусть в трехмерном пространстве с д.п.с.к. XYZ задана плоскость P.

Пусть: т. 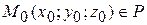– фиксированная точка P;

т. – «текущая» точка P;

вектор 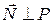, причем, .

Тогда скалярное произведение векторов 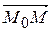и равно нулю, т.е. .

Учитывая проекции векторов 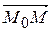и

,

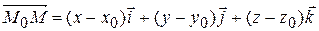получим

– уравнение плоскости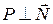

и проходящей через

т. .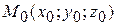

Преобразуем последнее уравнение

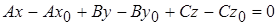или .

Обозначая 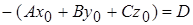, получим

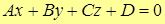– общее уравнение плоскости.