Прямая. Каноническое, параметрическое и общее уравнение прямой
Пусть в трехмерном пространстве с д.п.с.к. XYZ задана прямая L.
Пусть т. 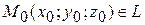 – фиксированная точка L;
– фиксированная точка L;
т. 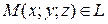 – «текущая» точка L.
– «текущая» точка L.
Пусть вектор 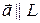 . Вектор
. Вектор 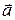 называют направляющим для прямой L. Пусть заданы координаты направляющего вектора, причем,
называют направляющим для прямой L. Пусть заданы координаты направляющего вектора, причем, 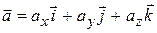 .
.
Рассмотрим вектор 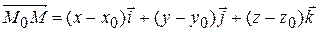 .
.
Так как по условию 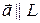 , то
, то 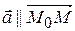 .
.
Условие параллельности двух векторов:
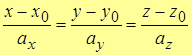 – каноническое уравнение прямой.
– каноническое уравнение прямой.

| Note 1 | Дома или на п/з (исходя из того, что вектор 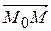 можно представить в виде можно представить в виде 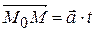 , где t – параметр) получить параметрическое уравнение прямой L: , где t – параметр) получить параметрическое уравнение прямой L:
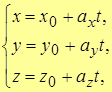 где где 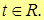
|
Дата добавления: 2015-08-20; просмотров: 743;
