Функция натурального аргумента
| Def. | Пусть каждому натуральному числу 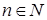 по какому-то закону поставлено в соответствие число по какому-то закону поставлено в соответствие число 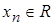 , то говорят, что задана функция натурального аргумента (переменная величина, числовая последовательность, …). , то говорят, что задана функция натурального аргумента (переменная величина, числовая последовательность, …).
|
Обозначение: 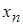 ,
, 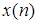 ,
, 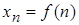 ,
, 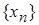 , …
, …
| n: | 1, | 2, | 3, | 4, | …, | n, | … |
| ↓ | ↓ | ↓ | ↓ | ↓ | |||
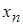 : :
| 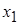 , ,
| 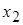 , ,
|  , ,
| 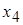 , ,
| …, | 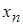 , ,
| … |
Мы будем применять первое обозначение, т.е. 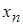 .
.
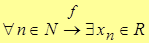 .
.
| Ex. 1. | Пусть задан закон 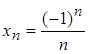 (задана числовая последовательность) тогда (задана числовая последовательность) тогда
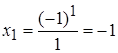 – первыйчлен последовательности; – первыйчлен последовательности;
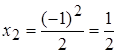 – второйчлен последовательности; – второйчлен последовательности;
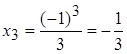 – третийчлен последовательности;
… – третийчлен последовательности;
…
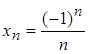 – n-й член последовательности (общий член последовательности).
… – n-й член последовательности (общий член последовательности).
…
|
Изображение. Члены последовательности изображают точками на плоскости (1-й способ) или точками на числовой прямой (2-й способ).
 Пусть задана числовая последовательность
Пусть задана числовая последовательность 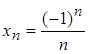 .
.
1-й способ

2-й способ
Мы будем применять 2-й способ изображения.
Дата добавления: 2015-08-20; просмотров: 1203;
