Основные теоремы о пределах
| Т. 1. | (О единственности предела). Если переменная имеет конечный предел, то он единственный. |
Proof:
Пусть переменная 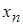 имеет два (различных, конечных) предела a и b. Пусть, например, a<b.
имеет два (различных, конечных) предела a и b. Пусть, например, a<b.
Тогда, по определению предела:
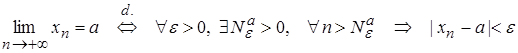 , (1)
, (1)
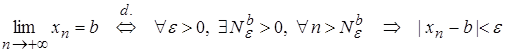 . (2)
. (2)
Выберем в качестве номера 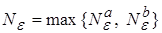 , тогда неравенства (1) и (2) выполняются.
, тогда неравенства (1) и (2) выполняются.
Пусть 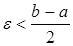 (такой выбор возможен, т.к. ε – любое, сколь угодно малое, положительное число).
(такой выбор возможен, т.к. ε – любое, сколь угодно малое, положительное число).
Тогда переменная 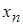 попадает в две непересекающиеся «ε-окрестности» т. a и т. b, что невозможно.
попадает в две непересекающиеся «ε-окрестности» т. a и т. b, что невозможно.
Полученное противоречие и доказывает теорему.
| Note 1 |  Дома или на п/з доказать:
Если (начиная с некоторого номера) выполняется неравенство Дома или на п/з доказать:
Если (начиная с некоторого номера) выполняется неравенство 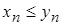 и и 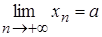 и и 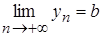 , то , то 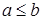 . .
|
| Т. 3. | Всякая сходящаяся числовая последовательность ограничена. |
Proof:
| Def. | Числовая последовательность 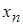 называется сходящей, если она имеет конечный предел. называется сходящей, если она имеет конечный предел.
|
| Def. | Числовая последовательность 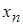 называется ограниченной, если называется ограниченной, если 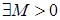 , такое, что для , такое, что для 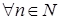 выполняется неравенство выполняется неравенство
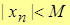 . .
|
Пусть числовая последовательность сходится. Это значит, что для 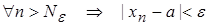 . Т.е. бесконечное множество членов последовательности попадает в «ε-окрестность» точки а, или лишь конечное число членов последовательности
. Т.е. бесконечное множество членов последовательности попадает в «ε-окрестность» точки а, или лишь конечное число членов последовательности 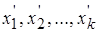 находится вне ее.
находится вне ее.
Пусть 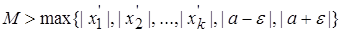 , тогда неравенство
, тогда неравенство 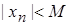 выполняется при
выполняется при 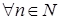 .
.

| Т. 4. | (Теорема о сжатой переменной или «правило двух милиционеров»)
Пусть, начиная с некоторого номера n выполняется двойное неравенство 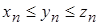 .
Пусть .
Пусть 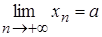 и и 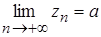 , тогда , тогда 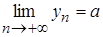 . .
|
Proof:
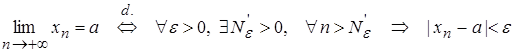 , (1)
, (1)
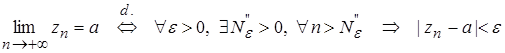 . (2)
. (2)
Выберем в качестве 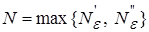 .
.
Тогда неравенства (1) и (2) – выполняются.
Учитывая, что 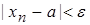
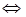
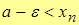
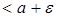 ,
,
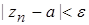
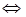
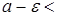
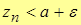 ,
,
и, оставляя левую часть первого неравенства и правую часть второго, получим
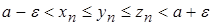
или
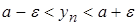 ,
,
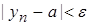 , что и требовалось доказать (ч.т.д.).
, что и требовалось доказать (ч.т.д.).
Графически это можно изобразить так.

| Т. 5. | Если числовая последовательность монотонно возрастает и ограничена сверху, то она имеет конечный предел. |
Proof:
Пусть числовая последовательность монотонно возрастает (в строгом смысле), т.е.
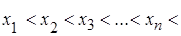 .
.
Пусть M – одна из верхних границ (очевидно, что таких верхних границ найдется бесконечное множество).
Пусть 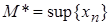 – точная верхняя грань множества
– точная верхняя грань множества 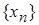 .
.
Докажем, что 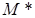 и есть предел переменной
и есть предел переменной 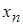 , т.е.
, т.е.
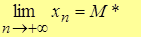
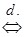
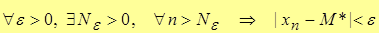 .
.
Так как неравенство
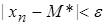
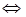
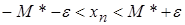 ,
,
то необходимо доказать, что, для 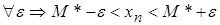 .
.
Левая часть неравенства выполняется, т.к. по условию теоремы 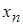 монотонно возрастает.
монотонно возрастает.
 Правая часть неравенства очевидна, т.к. M* – точная верхняя грань множества
Правая часть неравенства очевидна, т.к. M* – точная верхняя грань множества 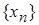 , ч.т.д.
, ч.т.д.
| Note 2 | Дома или на п/з доказать, что монотонно убывающая числовая последовательность, ограниченная снизу, имеет конечный предел. |
| Note 3 | Дома или на п/з доказать, что предел константы есть сама константа. |
Дата добавления: 2015-08-20; просмотров: 1413;
