Теорема о пределах
| Лемма | Если переменная имеет конечный предел, то она отличается от предела на б.м.в. |
Proоf:
.
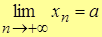
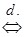
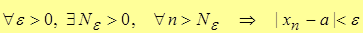Обозначим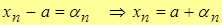 
, где 
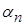– б.м.в.
Действительно, мы получили, что
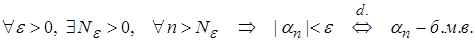, ч.т.д.
Пусть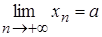 
, 
, 
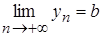с – const, тогда
| Т.1. |  .
|
| Т.2. |  .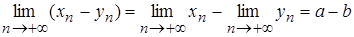
|
| Т.3. |  .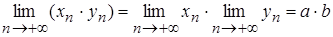
|
| Т.4. |  .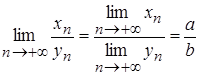
|
| Т.5. |  .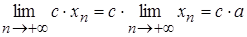
|
Докажем, например, Т.1.
Пусть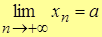 
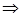
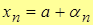, где 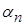– б.м.в.
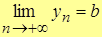
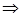
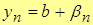, где 
– б.м.в.
Тогда
,
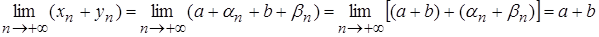ч.т.д.
| Note | Дома или на п/з доказать (аналогично) Т.2. – Т.5.. |
Дата добавления: 2015-08-20; просмотров: 575;