Кривые второго порядка в полярной системе координат
Пусть на плоскости задана д.п.с.к. X0Y и п.с.к. с полюсом 0 в т.O(0;0) и полярной осью OP, совпадающей с осью 0X.
Пусть кривые второго порядка расположены так, что полюс 0 совпадает:
– c фокусом F для параболы;
– с левым фокусом F1 для эллипса;
– с правым фокусом F2 для гиперболы.
 |
| Note | Напомним, что основной характеристикой кривой второго порядка является ее эксцентриситет 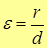 . .
|
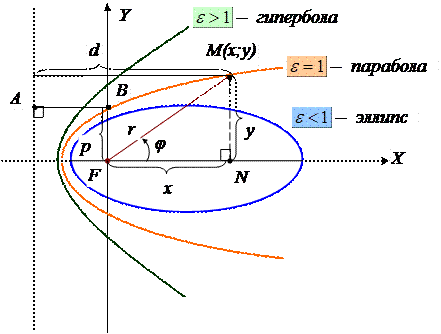
Приведем вывод формулы кривой второго порядка, например, для параболы.
Пусть: M(x;y) – «текущая» точка параболы;
|FM| =r – фокальный радиус;
|FB| = p – параметр, (p>0);
d – расстояние от т. М до директрисы;
B(0;p) – точка параболы.
Тогда  .
.
Для точки параболы 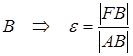 , где А – основание перпендикуляра, опущенного из т. В на директрису параболы.
, где А – основание перпендикуляра, опущенного из т. В на директрису параболы.
Учитывая, что 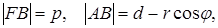 получим
получим  но так как
но так как 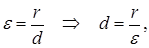 окончательно
окончательно  , или
, или 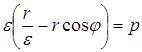 ,
, 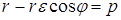 , откуда
, откуда
 – уравнение кривой второго порядка в п.с.к.
– уравнение кривой второго порядка в п.с.к.
Напомним, что если
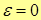 – окружность, – окружность,
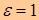 – парабола, – парабола,
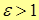 – гипербола, – гипербола,
 – эллипс. – эллипс.
|
Дата добавления: 2015-08-20; просмотров: 1506;
