Эллипс. Вывод канонического уравнения. Основные характеристики
| Def. | Эллипсом называют геометрическое место точек плоскости, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (бόльшая, чем расстояние между фокусами). |
Пусть 2с – расстояние между фокусами;
2а – постоянная величина (2a > 2c);
r1 – первое расстояние (левый фокальный радиус);
r2 – второе расстояние (правый фокальный радиус).
Очевидно, что c>0, a>0, r1>0, r2>0.
Тогда уравнение эллипса (по определению):
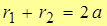 , причем
, причем 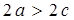 .
.
Получим уравнение эллипса в д.п.с.к. X0Y.
Расположим ось 0Х так, чтобы фокусы F1 и F2 принадлежали ей, ось 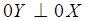 и начало координат 0 – являлось серединой отрезка [F1;F2].
и начало координат 0 – являлось серединой отрезка [F1;F2].
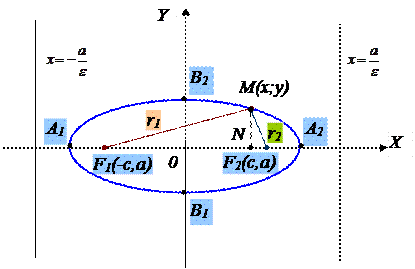
Тогда координаты фокусов – F1(-c;0), F2(c;0).
Пусть т. M(x;y) –«текущая» точка эллипса.
 | |||||
 |  |
По теореме Пифагора из прямоугольного ΔF1 MN:
 .
.
Из прямоугольного ΔF2 MN:
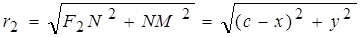 .
.
Учитывая, что 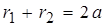 , получим
, получим

или
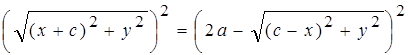 ,
,
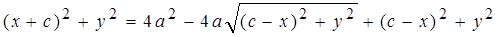 ,
,
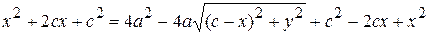 ,
,
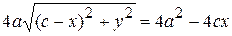 ,
,
 ,
,
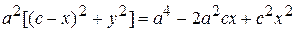 ,
,
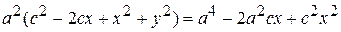 ,
,
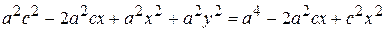 ,
,
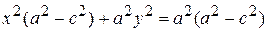 .
.
Обозначим  , т.к. a > c, тогда
, т.к. a > c, тогда
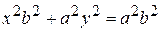 .
.
Или  – каноническое (простейшее) уравнение эллипса.
– каноническое (простейшее) уравнение эллипса.
Дата добавления: 2015-08-20; просмотров: 1250;
