Ранги матрицы(продолжение).

Ранг произведения матриц не выше рангов каждого из сомножителей.

mxn nxl mxl

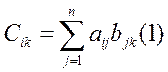
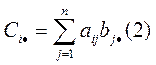i-ая строка C_iматрицы С является линейной комбинацией строк матрицы В

[C_1∙,C_2∙, _,C_m]⊂[b_1∙,b_2∙,…,b_n∙]⇒[C_M∙]⊂[B_N∙]⇒rangC≤rangB

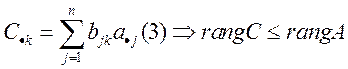
Следствие:

Ранг произведения произвольной матрицы А справа или слева на квадратную невырожденную матрицу Qравен рангу матрицы А.

а) C=AxQ⇒rangC≤rangA

|Q|≠0⇔∃Q^-1

CxQ^-1=AxQxQ^-1=A⇒rangA≤rangA⇒rangA=rangC

СЛАУ