Доказательство Т.3.

В силу Т.2 сумма любого частного решения системы(1) и любого решения системы(2), будет новым частным решением системы(1).

Берем любое решение системы(1) λ=(λ_j)

β=(β_j)тоже любое решение системы(1).

Фиксируем.

γ=λ-β(по Т.1)⇒решение системы(2) (по Т.2)⇒λ=λ+β

Линейные отображения векторных пространств(Морфизмы).

Обратное отображение – есть композиция fс g- это idна y, и наоборот idна x.

Рассмотрим 2 векторных пространства. V,W– векторные пространства на одном и том же числовом полем P(≡R_n,C_n)

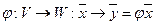
1. Говорят, что отображение φ линейно, если оно сохраняет линейные операции, т.е. образ суммы любых двух векторов равной сумме их образов.

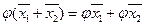
2. Произведение образ на число равно произведению образа этого вектора на число

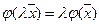
Теорема:Условие линейности 1.+2.⇒равносильны следующие условия:

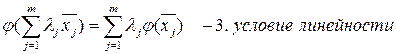
4. Образ любой линейной комбинации векторов равен линейной комбинации образов этих векторов с теми же самыми коэффициентами.

Отображение: Правило ставит (x, f, y) в соответствие элементу из первого множества – единственный элемент из второго множества.

Обратное отображение существует ó когда исходное отображение биективно.

Любой инъективный гоморфизм – мономорфизм.

Любой сюръективный гоморфизм – эпиморфизм.

Любой биективный гоморфизм – изоморфизм.

Два вектора пространства V и W называют изоморфными, если между ними можно установить изоморфное соответствие.

Координатный изоморфизм.

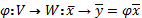– гомоморфизм.

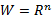
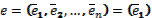– базис V.

;

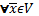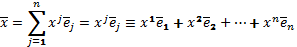
Соглашение о суммирование. Если в некотором выражении с индексом один и тот же индекс встречается два раза как верхний, так и нижний индекс, то предполагается, что по данному индексу в выражении произведено суммирование в данном (от e до n) отрезке.

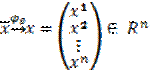(2)

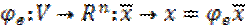
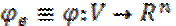– лин.

Координаты суммы равны сумме координат и с произведением на число.