Доказательство. Рассмотрим последовательность частичных сумм ряда с неотрицательными членами

Рассмотрим последовательность частичных сумм ряда с неотрицательными членами

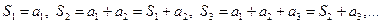
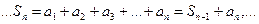
Учитывая, что все члены ряда неотрицательны, приходим к выводу о том. Что последовательность неубывающая, т.е.

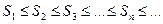
Так как последовательность ограничена сверху, то она имеет предел, что означает сходимость ряда (1).

Для решения вопроса о сходимости или расходимости ряда найдено много достаточных признаков. Рассмотрим некоторые из них.

Теорема 2.(первый признак сходимости)

Пусть имеются два ряда с неотрицательными членами

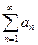(а)

и

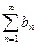, (b)

Причем члены ряда (а) с некоторого номера, не превосходят членов ряда (b)

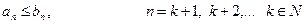(2)

Тогда из сходимости ряда (b) следует сходимость ряда (а). Из расходимости ряда (а) следует расходимость ряда (b).

Рассмотрим, сначала, случай 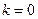, т.е. случай выполнения неравенства (2) для любых n. Тогда для частичных сумм рядов (а) и (b) будет выполняться неравенство.

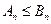(3)

Если ряд (b) сходится, то сходящаяся последовательность его частичных сумм ограничена, следовательно, последовательность частичных сумм ряда (а) ограничена сверху и по теореме 1 данного параграфа этот ряд будет сходиться.

Рассмотрим случай, когда ряд (а) расходится. Предположим, что и ряд (b) сходится. Тогда из неравенства (3) следует, что и ряд (а) должен сходиться. Получили противоречие, доказывающее второе утверждение теоремы.

В случае, когда вместо рядов (а) и (b) можно рассмотреть ряды, полученные из них путем отбрасывания 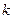первых членов, т.е. остатки этих рядов. По доказанному, утверждения теоремы будут справедливы для остатков рядов. Из материала предыдущего параграфа нам известно, что ряды и их остатки сходятся и расходятся одновременно, следовательно, теорема справедлива и в этом случае.