Необходимый признак сходимости числового ряда.

Теорема. Если ряд (1) сходится, то

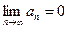(11)

Доказательство: Пусть S – сумма ряда. Выразим общий член ряда

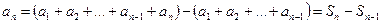
В последнем равенстве перейдем к пределу.

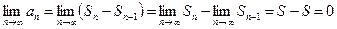
Теорема доказана.

Замечание. Из стремления общего члена к нулю еще не следует сходимость ряда.

Примеры.

1. Рассмотрим ряд ([2], часть 2, с. 247)

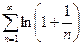(12)

Найдем предел общего члена

.

Необходимое условие выполнено. Найдем частичную сумму ряда

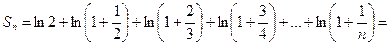
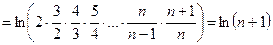
Найдем предел последовательности частичных сумм

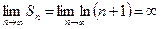
ряд расходится.

2. Исследовать на сходимость ряд .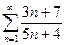

Вычислим предел общего члена ряда

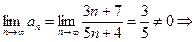ряд расходится.

3. Исследовать на сходимость ряд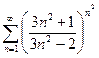

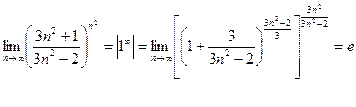
Следовательно, ряд расходится.

4. Рассмотрим гармонический ряд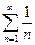

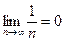, ряд может оказаться как сходящимся, так и расходящимся.

Пусть гармонический ряд сходится и сумма его равна S.

Тогда 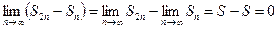, но с другой стороны:

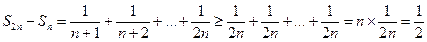
т.е. наше предположение неверно, ряд 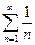расходится.