Примеры. - сходится, как геометрическая прогрессия, исходный ряд тоже сходится.
1. 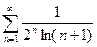
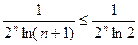
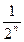 - сходится, как геометрическая прогрессия,
- сходится, как геометрическая прогрессия, 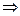 исходный ряд тоже сходится.
исходный ряд тоже сходится.
2. 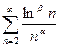 ;
; 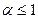 ;
; 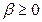
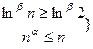
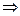
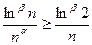 ,
, 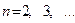 . Но
. Но 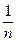 - расходится,
- расходится, 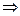
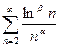 ;
; 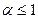 ;
; 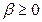 - расходится.
- расходится.
3. Исследовать на сходимость ряд 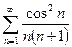 .
.
Из неравенства 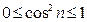 следует, что
следует, что
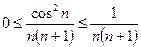
Рассмотрим частичную сумму ряда 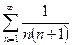 .
.
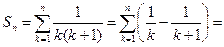
 .
.
Предел последовательности частичных сумм
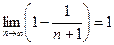 .
.
По определению ряд 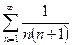 сходится, а следовательно по первому признаку сравнения сходится исследуемый ряд
сходится, а следовательно по первому признаку сравнения сходится исследуемый ряд 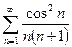 .
.
Теорема 3.(второй признак сходимости)
Пусть имеются два ряда с неотрицательными членами
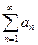 (а)
(а)
и
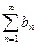 , (b)
, (b)
кроме того, существует конечный, отличный от нуля, предел
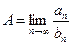
Тогда ряды (а) и (b) сходятся или расходятся одновременно.
Доказательство.
По условию теоремы 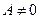 , т.к.
, т.к. 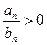 то
то 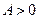 . Выберем произвольное
. Выберем произвольное 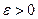 , но такое, что
, но такое, что 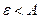 . Это означает, что
. Это означает, что 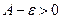
Из определения предела следует, что найдется такой номер 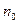 , что для всех
, что для всех 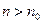
будет выполняться неравенство
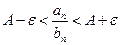 . (4)
. (4)
т.к. 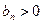 , то неравенство (4) можно записать в виде (5)
, то неравенство (4) можно записать в виде (5)
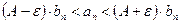 (5)
(5)
Если ряд сходится, то по свойствам сходящихся рядов сходится ряд 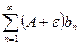 , тогда из неравенства (5) следует, что
, тогда из неравенства (5) следует, что 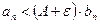 , тогда по первому признаку сходимости ряд
, тогда по первому признаку сходимости ряд 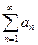 сходится.
сходится.
Если ряд 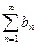 расходится, то расходится и ряд
расходится, то расходится и ряд 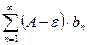 . Из неравенства (5) следует, что
. Из неравенства (5) следует, что 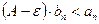 тогда согласно первому признаку сходимости будет расходиться ряд
тогда согласно первому признаку сходимости будет расходиться ряд 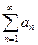 .
.
Проводя аналогичные рассуждения можно доказать, что из сходимости ряда 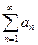 следует сходимость ряда
следует сходимость ряда 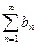 , а из расходимости ряда
, а из расходимости ряда 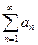 следует расходимость ряда
следует расходимость ряда 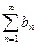 .
.
Дата добавления: 2015-08-11; просмотров: 713;
