Простейшие свойства сходящихся рядов.

Интернет-ресурсы

1. www.exponenta.ru

Теоретическая часть

Тема 1. Числовые ряды и их приложения.

Основные понятия и простейшие свойства рядов

Определение: Пусть имеется бесконечная последовательность чисел , . Сумма в сокращенной записи 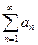(1) называется числовым рядом.

Примеры:

1. Выписать первые 4 члена ряда: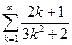

=

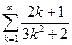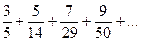
2. Подобрать один из возможных вариантов формулы общего члена ряда:

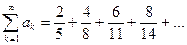
Числители дробей являются первыми четными числами: 2,4,6,8…

Можно предположить, что числитель дроби, соответствующий k-му члену данного ряда, будет k-е по счету четное число: 2k.

Знаменатели дробей являются первыми четырьмя членами арифметической прогрессии с разностью, равной 3, и первым членом равным 5.

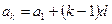
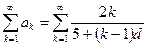
Это возможный вариант, но не единственный.

Числа называются членами ряда.

Выражения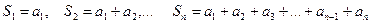

называются частичными суммами ряда (1). Частичные суммы образуют числовую последовательность.

Определение.Если существует конечный предел последовательности n-х частичных сумм , (2)

то он называется суммой ряда (1).

Если S, конечное число, то ряд называется сходящимся. Если же предел (2) бесконечен или не существует, то ряд называется расходящимся.

В качестве примера рассмотрим сумму бесконечной геометрической прогрессии

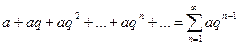
Из элементарной математики известна формула суммы n членов прогрессии (n-ая частичная сумма в нашей терминологии), полученная в предположении, что .

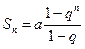
Если 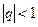, то и ряд будет сходящимся.

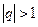Если , то 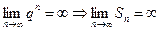, соответственно ряд будет расходящимся.

Если 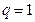, то .

Наконец, если , то частичная сумма с четного числа слагаемых

,

а частичная сумма нечетного числа слагаемых будет равна 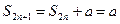. Последовательность таких частичных сумм предела не имеет и ряд в этом случае также расходящийся.

Примеры:

Найти сумму ряда:

1.

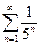
Данный ряд представляет собой сумму бесконечно убывающей геометрической прогрессии с первым членом 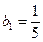и знаменателем , а значит, сумму его можно найти по формуле суммы бесконечно убывающей геометрической прогрессии

.

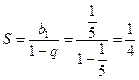2.

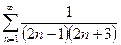
Разложим общий член ряда на простые дроби:

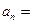
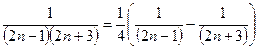, (можно воспользоваться методом неопределенных коэффициентов), вычислим n-ю частичную сумму ряда: тогда по определению суммы ряда

.

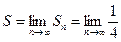
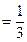3.

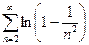
Вычислим n-ю частичную сумму ряда:

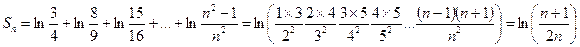, тогда .

Простейшие свойства сходящихся рядов.

1. Пусть ряд

(3)

сходится и его сумма равна S, тогда ряд

(4)

также сходится и его сумма равна .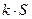

Доказательство: Рассмотрим частичные суммы рядов (3) и (4). Имеем

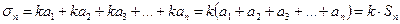
Так как ряд (3) сходится, то существует конечный предел последовательности его частичных сумм равный S, тогда

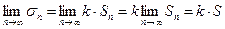
Последнее равенства и доказывает свойство.

2. Пусть имеются два сходящихся ряда:

(5)

и

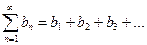(6)

Пусть А и В – суммы этих рядов. Тогда ряд

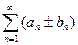
также сходится и его сумма равна .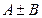

Доказательство

Рассмотрим частичные суммы последнего ряда

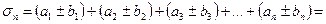
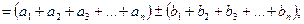
Найдем предел последовательности частичных сумм

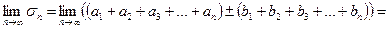
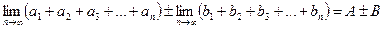
При нахождении пределов мы воспользовались сходимостью рядов (5) и (6).

4. ОпределениеЧисловой ряд

,

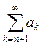полученный из ряда (1) путем отбрасывания первых n членов, называется остатком ряда (1). Принято обозначение:

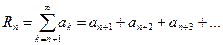(8)

Имеет место следующее утверждение:

Если ряд (1) сходится, то сходится любой из его остатков.

Справедливо и обратное утверждение

Если сходится хотя бы один из остатков ряда, то сходится и сам ряд.

Обозначим 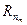частичную сумму ряда (8), ее можно представить в виде

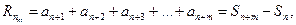
где 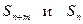- частичные суммы ряда (1). Можно записать

(9)

Зафиксируем число n. Если ряд (1) сходится, то для любого n, существует предел , тогда из равенства (9) будет следовать существование предела 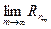, что означает сходимость остатка (8).

Используя равенство (9) и проводя аналогичные рассуждения, можно доказать обратное утверждение.

Докажем еще одно свойство остатков сходящегося ряда.

Если ряд (1)сходится, то последовательность сумм его остатков стремится к нулю, т.е.

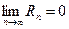
Доказательство. В следствие сходимости ряда (1), приходим к равенству

, (10)

где за S обозначена сумма ряда (1). По определению . Переходим к пределу в равенстве (10)

.