Интегральный признак Коши. Теорема (интегральный признак Коши).

Теорема (интегральный признак Коши).

Пусть имеется ряд с положительными монотонно убывающими членами

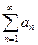(1)

и пусть 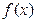непрерывная, положительная, монотонно убывающая функция, такая что

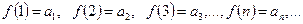(2)

Тогда

1) Если несобственный интеграл 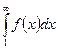сходится, то сходится и ряд (1);

2) Если указанный интеграл расходится, то расходится и ряд (1).

Для доказательства рассмотрим геометрическую интерпретацию интеграла и частичных сумм ряда (1).

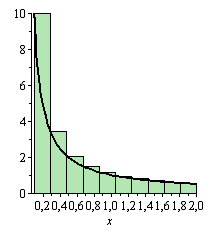
Рисунок 1 поясняет тот факт, что площадь ступенчатой фигуры равна (т.к. площадь одного прямоугольника равна произведению соответствующего члена ряда- высоты на единицу – длину основания)

.

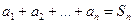С другой стороны, площадь криволинейной трапеции, ограниченной графиком функции, прямыми 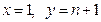и осью ОХ можно вычислить с помощью определенного интеграла 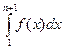. Имеем неравенство

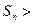
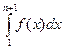(3)

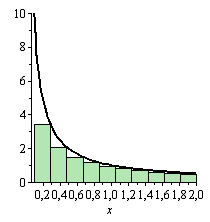
На втором рисунке площадь ступенчатой фигуры

.

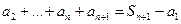В результате приходим к неравенству

,

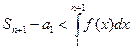Тогда

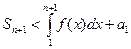(4)

Теперь рассматриваем случай, когда несобственный интеграл сходится, тогда существует конечная величина

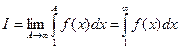
Так как

,

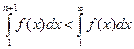с учетом неравенства (4), получаем

.

Следовательно, возрастающая последовательность частичных сумм ряда (1) ограничена сверху, значит, она имеет предел, а ряд, по определению, сходится.

Если интеграл расходится, т.е.

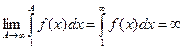
из неравенства (3) будет следовать, что последовательность частичных сумм неограниченно возрастает, следовательно, ряд (1) расходится.