Доказательство

Равенство а) легко проверяется, поскольку функция 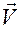линейно зависит от .

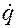Равенство б) проверяется непосредственным вычислением его левой и правой части.

Вычисляя левую часть равенства б) в формулировке леммы Лагранжа, получим:

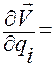
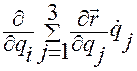
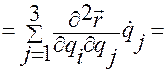
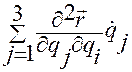. (1.5.36)

Последнее равенство в соотношении (1.5.36) записано на основе того, что:

функция 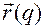дважды непрерывно дифференцируема по переменным .

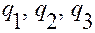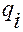А тогда смешанные производные от по и 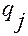будут непрерывными и, следовательно, порядок дифференцирования при их вычислении можно переставлять.

При такой перестановке значения смешанных производных будут совпадать:

.

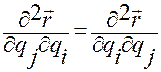Сопоставляя (1.5.36) и (1.5.35)

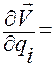
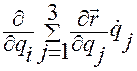
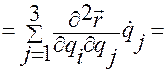
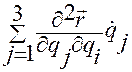, (1.5.36)

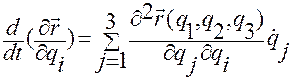, (1.5.35)

видим, что правая и левая части равенства б) совпадают.

Лемма доказана.

В заключение отметим, что в Дополнении 1.2 к §5 в п.п. 8.6 и 8.7 дается другой вывод формулы вычисления ковариантных координат скорости, а также описывается связь декартовых координат скорости с обобщенными скоростями.