Лемма Лагранжа

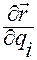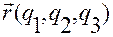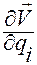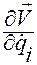Установим теперь связь производных от функции с производными и от функции .

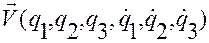Такая связь дается леммой Лагранжа.

Лемма Лагранжа

При всех 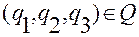и любых значениях переменных 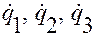выполняются равенства

а) , ;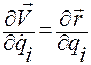

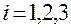б) , .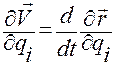

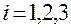Здесь 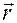задается формулой (1.5.1), 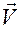— формулой (1.5.32), а 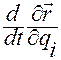— правой частью равенства (1.5.35).