Лекция 15 УРАВНЕНИЯ ЛАГРАНЖА II-ГО РОДА

Обобщенные координаты системы. Обобщенные силы
и способ их вычисления. Уравнения Лагранжа II-го рода

Обобщенными координатами механической системы называются величины, заданием которых вполне определяется положение всех точек системы.

Числом степеней свободы системы называется число независимых обобщенных координат, определяющих положение точек системы.

Рассмотрим механическую систему, состоящую из п материальных точек М₁, М₂, … М_п, имеющую К степеней свободы. Обозначим ее независимые обобщенные координаты q₁, q₂, … q_k. Они вполне определяют положение всех точек системы. Тогда декартовы координаты системы будут функциями обобщенных координат:

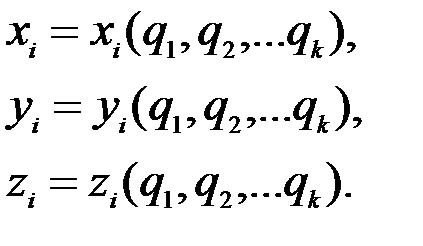
Эти соотношения имеют место только в том случае, когда связи не зависят от времени. Возможно существование связей, изменяющихся с течением времени.

Пример: нить маятника тянут за конец А с постоянной скоростью V.

Пусть ОМ = l , тогда ,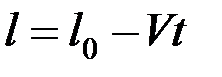

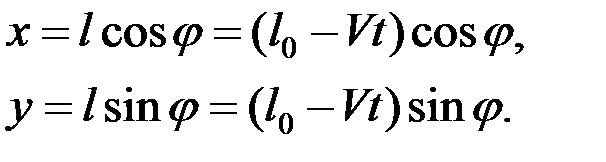
Очевидно, что в данной задаче декартовы координаты – не только функции обобщенной координаты j, но и времени t.

В этом случае имеем:

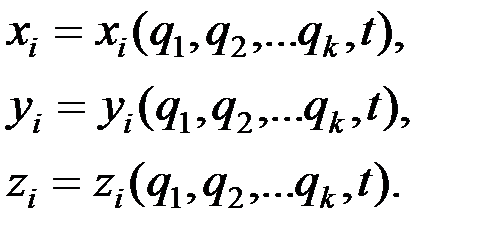
Связи, не зависящие от времени, называются склерономными (или стационарными), а изменяемые с течением времени – реономными (или нестационарными).