Обобщенные силы
Рассмотрим механическую систему, состоящую из п материальных точек: М1, М2, … Мп, имеющую К степеней свободы. Обозначим ее независимые обобщенные координаты q1, q2, … qk. Предположим, что к точкам системы приложены силы 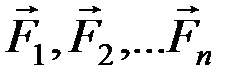 . Чтобы вычислить обобщенную силу, дадим координате q1 ничтожно малое приращение dq1 , оставляя прочие координаты без изменения. Это изменение координаты q1 вызовет ничтожно малые перемещения e1, e2, eп всех точек системы. Вычислим сумму работ сил
. Чтобы вычислить обобщенную силу, дадим координате q1 ничтожно малое приращение dq1 , оставляя прочие координаты без изменения. Это изменение координаты q1 вызовет ничтожно малые перемещения e1, e2, eп всех точек системы. Вычислим сумму работ сил 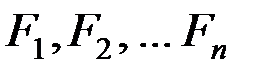 на перемещениях e1, e2, eп:
на перемещениях e1, e2, eп:
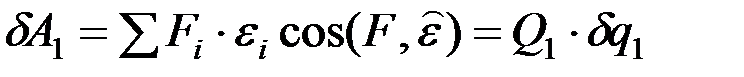 .
.
Пусть эта работа равна произведению некоторого множителя Q1на приращение координаты dq1. Поступая аналогично, найдем Q2, … Qk, соответствующие координатам q2, … qk:
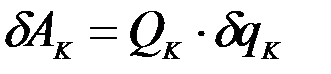 .
.
Обобщенная сила – это величина, равная коэффициенту при приращении обобщенной координаты в выражении полной элементарной работы действующих на систему сил.
Не следует считать, что обобщенная сила всегда имеет размерность [Ньютон]. Работа всегда вычисляется в джоулях (1 Дж =1 Н×м).
| Размерность обобщенной координаты | Размерность обобщенной силы |
| м | Н |
| рад | Н×м |
| м3 | Па |
В механической системе с идеальными связями обобщенные реакции связей всегда равны нулю, поэтому при переходе к обобщенным силам реакции связей автоматически выпадают из расчетов. В этом большое преимущество методов Лагранжа.
Дата добавления: 2015-08-08; просмотров: 1772;
