Примеры вычисления обобщенной силы

К барабану 1 радиуса R приложен момент М, под действием которого осуществляется подъем груза 2. Массы барабана и груза соответственно равны т₁ и т₂.

Представленная на рисунке механическая система имеет одну степень свободы. Для определения обобщенной силы выберем в качестве обобщенной координаты угол поворота барабана – j (направим его против часовой стрелки). Дадим обобщенной координате приращение dj и вычислим полную элементарную работу всех активных сил на этом перемещении:

.

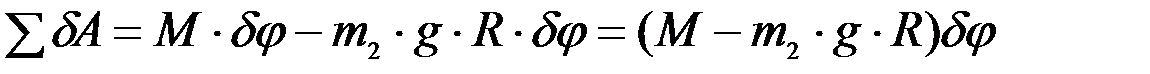Работа от веса барабана равна нулю, т.к. ось его вращения не перемещается. Тогда обобщенная сила равна .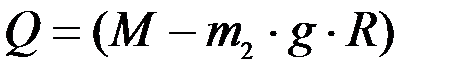

Другой пример. Пусть система материальных точек М₁, М₂, М₃, … М_п имеет k степеней свободы. Обозначим ее обобщенные координаты q₁, q₂, … q_k. Возьмем декартовы оси x, y, z и обозначим координаты точки М_i через 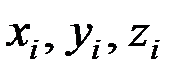. Координаты являются функциями обобщенных координат и времени:

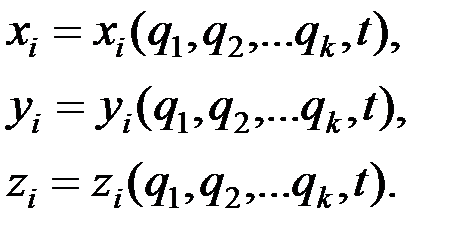
К системе приложены силы 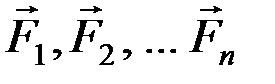. Вычислим обобщенные силы 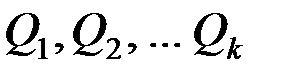. Например, .

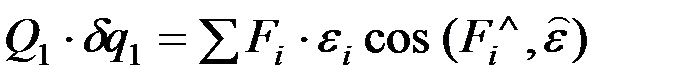Элементарную работу силы F_i мы можем вычислить как

.

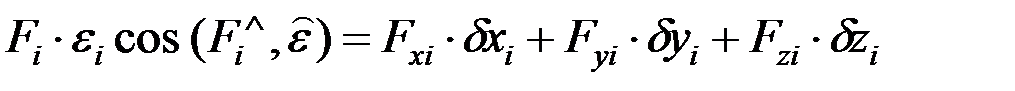Т.к. 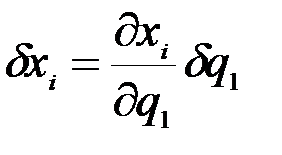, , 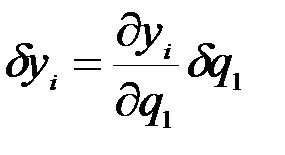, то

.

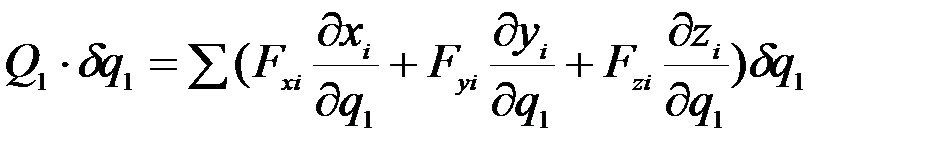Рассуждая аналогично и поделив обе части равенства на dq, получим:

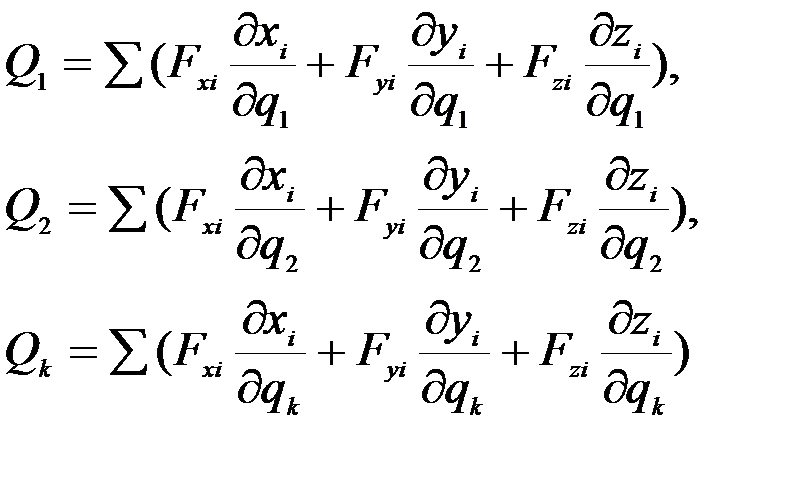
или

.