Основное уравнение теории удара
При движении тела под действием сил, которые до сих пор рассматривались, скорости точек тела изменяются непрерывно, т. е. за любой бесконечно малый промежуток времени скорость получает бесконечно малое приращение. Этот результат непосредственно следует из теоремы об изменении количества движения.
Действительно, допустим, имеется точка с массой т, на которую действуют силы 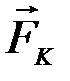 (К = l, 2, ... , п). Представим импульс любой из этих сил за промежуток времени t в виде
(К = l, 2, ... , п). Представим импульс любой из этих сил за промежуток времени t в виде 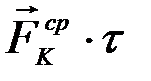 , где
, где 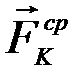 есть среднее значение силы за время t. Тогда теорема об изменении количества движения этой точки дает:
есть среднее значение силы за время t. Тогда теорема об изменении количества движения этой точки дает:
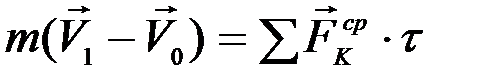 .
.
Отсюда видно, что, если время t бесконечно мало (стремится к нулю), то при обычных силах и приращение скорости 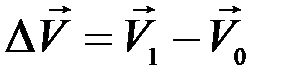 будет тоже величиной бесконечно малой (стремящейся к нулю).
будет тоже величиной бесконечно малой (стремящейся к нулю).
Однако, если в числе действующих сил будут очень большие силы (порядка 1/τ), то приращение скорости за малый промежуток времени окажется величиной конечной.
Явление, при котором скорости точек тела за очень малый промежуток времени t изменяются на конечную величину, называется ударом.
Силы, при действии которых происходит удар, будем называтьударными силами 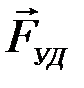 . Очень малый промежуток времени t, в течение которого происходит удар, назовем временем удара.
. Очень малый промежуток времени t, в течение которого происходит удар, назовем временем удара.
Так как ударные силы очень велики и за время удара изменяются в значительных пределах, то в теории удара в качестве меры взаимодействия тел рассматривают не сами ударные силы, а их импульсы, которые называют ударными импульсами. Величина ударного импульса определяется равенством:
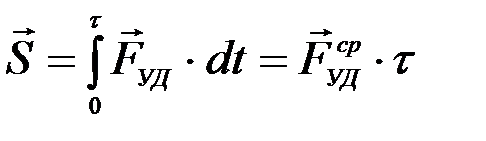 (1)
(1)
Из определения следует, что ударный импульс 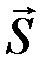 будет величиной конечной. Импульсы неударных сил за время t будут величинами очень малыми и ими можно пренебречь. Будем в дальнейшем обозначать скорость точки в начале удара
будет величиной конечной. Импульсы неударных сил за время t будут величинами очень малыми и ими можно пренебречь. Будем в дальнейшем обозначать скорость точки в начале удара 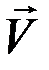 , а скорость в конце удара
, а скорость в конце удара 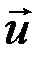 . Тогда равенство (1) примет вид:
. Тогда равенство (1) примет вид:
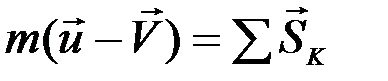 . (2)
. (2)
Этот результат выражает теорему об изменении количества движения точки при ударе:изменение количества движения материальной точки за время удара равно сумме действующих на точку ударных импульсов.
Уравнение (2) являетсяосновным уравнением теории удара.
Отметим, что перемещение точки за время удара будет равно 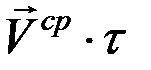 , где
, где 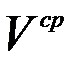 – среднее значение скорости за время t. Так как t очень мало, то это перемещение будет также величиной очень малой, которой практически можно пренебречь. Итак, из всех полученных результатов вытекает:
– среднее значение скорости за время t. Так как t очень мало, то это перемещение будет также величиной очень малой, которой практически можно пренебречь. Итак, из всех полученных результатов вытекает:
1) действием неударных сил (таких, например, как сила тяжести) за время удара можно пренебречь;
2) перемещениями точек тела за время удара можно пренебречь и считать тело во время удара неподвижным;
3) изменение скоростей точек тела за время удара определяется основным уравнением теории удара (2).
Дата добавления: 2015-08-08; просмотров: 1234;
