Утверждение.

Результатом такого построения будет союзная система, совпадающая с изначально заданной основной системой.

Коротко это утверждение формулируется так:

«Союзная система к союзной совпадает с основной».

Утверждение будет доказано, если покажем, что

,

,

,

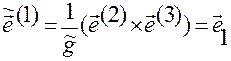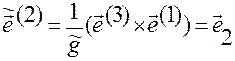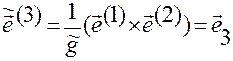где .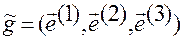

Докажем, например, справедливость первой формулы (остальные — доказываются аналогично).

Выше было установлено (см. (1.5.19)):

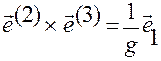. (1.5.19)

Кроме того, из (1.5.18) (свойство 2):

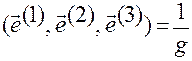(1.5.18)

имеем

.

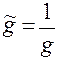Поэтому для вектора 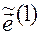можем записать

,

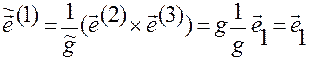что и требовалось доказать.

Из доказанных свойств, в частности, вытекает, что если основной базис является ортонормированным ортогональным базисом, то союзная система координат совпадает с основной.

В таком случае ковариантные координаты вектора 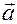(величины 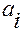) совпадают с соответствующими контравариантными координатами (величинами ).

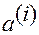Ниже в Дополнении 1.1 к §5 даются пояснения смысла терминов «контравариантные» и «ковариантные» координаты.