Доказательство. Подставим обратную матрицу А-1 = Ã - матричное уравнение (3.2.3), записав все матрицы в развернутой форме

Подставим обратную матрицу А^-1 = 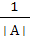Ã - матричное уравнение (3.2.3), записав все матрицы в развернутой форме

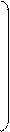
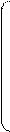
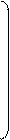
x₁ A₁₁ A₂₁ ... A_n1 b₁

x₂ A₁₂ A₂₂ …A_n2 b₂

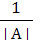- = - - - - - - - _(3.2.5)

- - - - - - - -

x_n A_1n A_2n …A_nn b_n

учитывая, что │А│= ∆, после умножения матриц получаем:

x₁ b₁ A₁₁ + b₂ A₂₁ + … + b_n A_n1

x₂ b₁ A₁₂ + b₂ A₂₂ + … + b_n A_n2

- = - - - - - - - - - - -

- - - - - - - - - - - -

x_n b_n A_1n + b_n A_2n+ …. + b_n A_nn

отсюда следует, что для любого j=1,n

x_j= 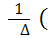b₁A_1j+ b₂A_2j+…+ b_nA_nn) (3.2.6)

Но на основании свойства определителей выражение, стоящее в скобках равенства (3.2.5) представляет собой определитель ∆_j для j=1,n. Следовательно, X_j= 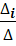. Теорема Крамера доказана.

Пример.Решить систему уравнений

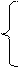х₁ + 2х₂ + х₃ = 8

-2х₁ + 3х₂ -3х₃ = -5

3х₁- 4х₂ + 5х₃=10

а) матричным способом; б) по формулам Крамера.