Собственные векторы и

собственные значения матрицы.

Определение.Вектор 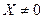называется собственным вектором квадратной матрицы 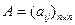, если существует такое число λ, что выполняется условие 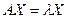. (3.1.6)

Число λ называется собственным значением (числом) матрицы, соответствующим вектору Х.

Из определения следует, что при умножении матрицы А на вектор Х получается вектор, коллинеарный вектору Х.

Равенство (3.6) перепишем в матричной форме.

,

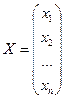тогда равенство (3.1.6) переходит в систему линейных уравнений

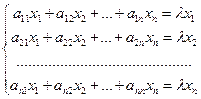
или 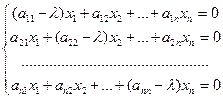(3.1.7)

В матричной форме система (3.1.7) имеет вид .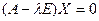

Чтобы однородная система (3.1.7) (или матричное уравнение (3.1.6)) имела ненулевое решение, необходимо и достаточно, чтобы ее определитель 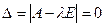, то есть

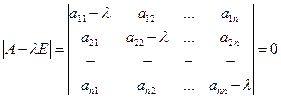(3.1.8)

Определитель 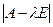представляет собой многочлен n-ой степени относительно λ. Он называется характеристическим многочленом матрицы А,а уравнение (3.1.8) характеристическим уравнением матрицы А.

Пример. Найти собственные значения и собственные векторы матрицы .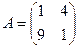

Решение.Составим характеристическое уравнение

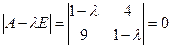или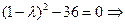

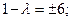
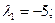
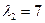
Находим собственные векторы (см. )

а) для собственного числа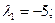

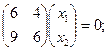
Оба уравнения совпадают. Одно следует отбросить. Система имеет бесчисленное множество решений. Положив , получаем 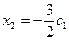. Собственному значению 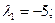соответствует собственные векторы .

б) Аналогично находится вторая совокупность собственных векторов .

В частности, это могут быть векторы 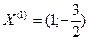и .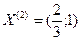

Со свойствами собственных чисел можно познакомиться в …

Закончить!