Определение.Совокупность n линейно независимых векторов n-мерного векторного пространства называется базисом.
Для базисных векторов 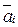 принято обозначение
принято обозначение 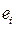 .
.
Справедлива следующая теорема.
Теорема. Каждый вектор Х векторного пространства можно представить, причем единственным образом, как линейную комбинацию базисных векторов 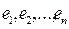 , то есть
, то есть  . ( 3.1.5)
. ( 3.1.5)
Доказательство.Пусть векторы 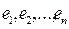 образуют некоторый базис n-мерного пространства. Тогда с любым вектором добавленным (
образуют некоторый базис n-мерного пространства. Тогда с любым вектором добавленным ( 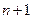 )-м вектором Х получаем совокупность линейно зависимых векторов. Это означает, что
)-м вектором Х получаем совокупность линейно зависимых векторов. Это означает, что 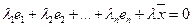 (
( 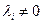 ), следовательно
), следовательно
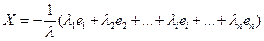
Обозначим 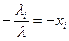 , откуда
, откуда 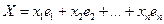 , что и требовалось доказать. Можно доказать, что полученное разложение является единственным.
, что и требовалось доказать. Можно доказать, что полученное разложение является единственным.
Пример. Даны векторы е1 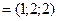 , е2
, е2 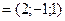 , е3
, е3  ,
, 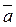
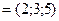 . Разложить вектор
. Разложить вектор 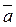 по базисным векторам
по базисным векторам  : запишем разложение вектора
: запишем разложение вектора 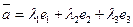 . Перейдем к координатной форме
. Перейдем к координатной форме
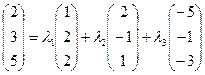
Перейдем к системе уравнений
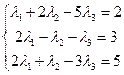
Решив систему любым методом (например, методом Крамера), получим ее решение: 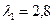 ,
, 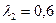 ,
, 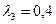 . Разложение вектора
. Разложение вектора 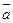 по базису имеет вид
по базису имеет вид 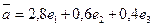 .
.
Дата добавления: 2015-08-14; просмотров: 1038;
