ВЕКТОРЫ В КООРДИНАТНОЙ ФОРМЕ
6.1. Составляющая вектора по числовой оси
Составляющей вектора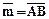 
по числовой оси OWбудем называть
вектор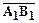 
, соединяющий проекции его начала и конца на данную ось.
6.1.1. Составляющую вектора по числовой оси можно найти с помощью
орта этой оси:
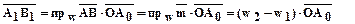
6.1.1.1.В прямоугольной декартовой системе координат орты координатных осей обозначают так: 
- орт оси OX , 
- орт оси OY , 
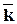- орт оси OZ.
Орты задают направление и масштаб числовых осей.
6.1.1.2. Углы между любым вектором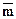 
и осями координат (или ортамикоординатных осей) обозначают так: 
.
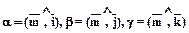6.1.1.3. Направляющими косинусами вектора 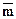будем назвать косинусы угловмежду этим вектором и осями координат : 
.
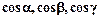6.1.2. В прямоугольной декартовой системе координат составляющие
любого вектора 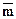можно найти по формулам:
- составляющая вектора 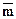по оси абсцисс 
;
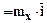- составляющая вектора 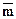по оси ординат 
;
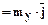- составляющая вектора 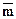по оси аппликат 
.
6.2. Разложение вектора на составляющие по координатным осям
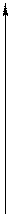Z
z2 
B3
В
z1 A3 
A
O A2 B2
y1 y2 Y
х1 А1 А0
х2 В0
Х
6.2.1. Любой вектор равен сумме всех своих составляющих по осям координат.
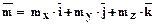- разложение вектора на составляющие по координатным осям.
6.2.2. Для того, чтобы задать вектор, достаточно задать все его координаты.
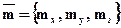- задание вектора в координатной форме;
тогда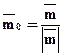 
- вектор единичной длины сонаправленный с , т.е.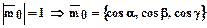 
- задание единичного вектора в координатной форме.
6.2.3. Действия с векторами в координатной форме
Пусть векторы заданы своими координатами:
; 
; 
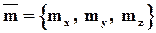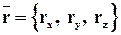;- скаляр.
6.2.3.1.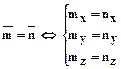 
6.2.3.2. 
6.2.3.3.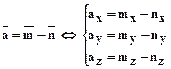 
6.2.3.4. 
6.2.3.5. 
6.2.3.6.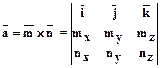 
6.2.3.7.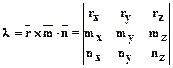 
.
6.2.3.8. 
.
6.2.3.9.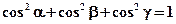 
.
Дата добавления: 2015-08-26; просмотров: 1507;