ПРЯМАЯ НА ПЛОСКОСТИ
 Пусть задана функция
Пусть задана функция 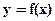 ,которая определена и непрерывна в некотором промежутке
,которая определена и непрерывна в некотором промежутке 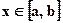 . В прямоугольной декартовой системе координат этой функции соответствует некоторое множество точек, которое будем называть линией на координатной плоскости, а равенство (*)
. В прямоугольной декартовой системе координат этой функции соответствует некоторое множество точек, которое будем называть линией на координатной плоскости, а равенство (*) 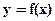 - уравнение этой линии.
- уравнение этой линии.
Если в уравнении линии все члены равнения перенести в левую часть, то получим уравнение вида (**) 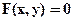 - уравнение линии на плоскости в неявном виде.
- уравнение линии на плоскости в неявном виде.
Если в уравнении переменные xиy расположены в разных слагаемых и только в первой степени, то такое уравнение называют линейным, это всегда уравнение прямой линии на плоскости.
Если в уравнении переменные находятся в разных слагаемых, причём в каждом только в виде: либо х2 , либо y2 , либо ху,тогда уравнение называют квадратным, а соответствующую линию – кривая второго порядка.Существует всего 4 вида кривых второго порядка: окружность, эллипс,гипербола,парабола.
Прямая линия задаётся своими свойствами и в зависимости от используемых свойств изменяется вид уравнения прямой.
9.1. Уравнение прямой, проходящей через две заданные точки 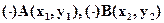


 Y
Y

 y2 B
y2 B



 y1 A
y1 A
 O X
O X
x1 x2
L
9.2. Уравнение прямой с угловым коэффициентом: 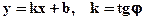

 Y L
Y L
φ
 b
b
 O X
O X
9.3. Уравнение прямой в отрезках на координатных осях: 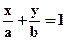
 Y
Y
 L
L
B B
 O A X
O A X
a
9.4.Уравнения прямых, параллельных координатным осям: 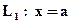 и
и 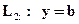

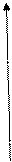 Y L1
Y L1
L2 b
 | |||
 |
O a X
9.5. Уравнения координатных осей: 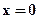 и
и 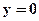 .
.
9.6. Общее уравнение прямой: 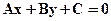 .
.
9.7.Если прямые L1иL2 заданы уравнениями 
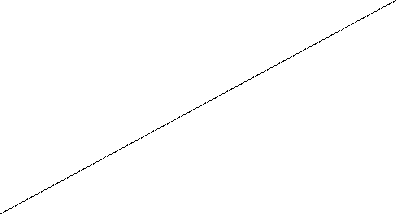
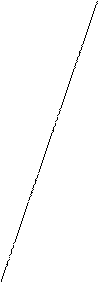 а угол между ними
а угол между ними 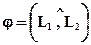 , то угол между ними можно вычислить по формуле
, то угол между ними можно вычислить по формуле 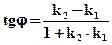

 Y
Y
φ
 φ
φ
 | |||
 | |||
φ1 φ2
 O X
O X
L1
L2
9.8. Условие параллельности двух прямых: 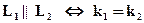 .
.
9.9. Условие перпендикулярности двух прямых:  .
.
ОГЛАВЛЕНИЕ
| Глава | Стр. | |
| Литература | ||
| Основные обозначения | ||
| Числовые множества | ||
| Матрицы | ||
| Определители | ||
| Векторы в геометрической форме | ||
| Метод координат | ||
| Векторы в координатной форме | ||
| Системы линейных уравнений | ||
| Метод полного исключения | ||
| Прямая линия на плоскости | ||
| Оглавление |
Дата добавления: 2015-08-26; просмотров: 641;
