МЕТОД КООРДИНАТ
Метод координат - это способ, с помощью которого осуществляется соответствие между точками (геометрическими элементами математики) и вещественными числами (аналитическими элементами). Для осуществления этого соответствия обычно используют числовую ось.
5.1. Понятие числовой оси
Числовой осью (L) или числовой прямой, будем называть прямую линию, удовлетворяющую следующим условиям:
- на прямой Lфиксируем 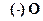 , называем ее началом координат и ставим ей в соответствие число 0;
, называем ее началом координат и ставим ей в соответствие число 0;
- точка О делит прямую на два направления (луча), одно из которых помечаем стрелкой и считаем положительным, а другое - отрицательным;
- на положительном направлении OLпостроим 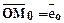 , единичной длины и назовем его орт числовой оси OL;
, единичной длины и назовем его орт числовой оси OL;
- каждой точке М, лежащей на данной прямой ставим в соответствие вещественное число w, которое определяется следующим образом:
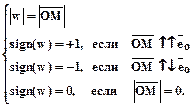
Число t назовем координатой точки Ми обозначим: 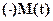 .
.
N(-2) O  M0 M(+3)
M0 M(+3)









 L
L
-2 -1 0 1 2 3
Из определения числовой оси следует, что между точками на числовой оси и вещественными числами установлено взаимно-однозначное соответствие, а именно:
любой точке на оси соответствует единственное вещественное число и любому вещественному числу соответствует единственная точка на числовой оси.
Точку на числовой оси будем считать заданной, если известна ее координата.
Чтобы найти точку на числовой оси достаточно найти ее координату.
5.2. Метод координат на числовой прямой
5.2.1. Расстояние между двумя точками
Дано: OL - числовая ось
 М1(х1) ,
М1(х1) ,  М2(х2)
М2(х2) 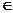 OL
OL 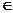
Найти: d= | M1M2 |
Ответ: 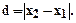
5.2.2. Деление отрезка в данном отношении
Дано: OL - числовая ось
 М1(х1),
М1(х1),  М2(х2)
М2(х2) 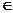 OL
OL
 М
М 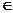 OL
OL
|M1M| : |MM2| = 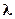
Найти:  М(х)
М(х)
Ответ: 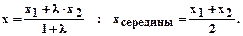
5.3. Метод координат на плоскости
Метод координат на плоскости устанавливает взаимно однозначное соответствие между точками плоскости и упорядоченными парами вещественных чисел (координатами точки).
5.3.1. Прямоугольная декартова система координат
Прямоугольная декартова система координат на плоскости представляет собой две взаимно перпендикулярные числовые прямые с общим началом координат.
 Y – ось ординат
Y – ось ординат
y M2 M

M1
 O x X - ось абсцисс
O x X - ось абсцисс
XOY -координатная плоскость,
 М1(х,0) - пр ох
М1(х,0) - пр ох  М; х - абсцисса точки М;
М; х - абсцисса точки М;
 М2(0,y) - пр оу
М2(0,y) - пр оу  М ; у - ордината точки М.
М ; у - ордината точки М.
Точка на плоскости считается заданной, если известны ее координаты.
5.3.1.2. Расстояние между двумя точками
Дано: ХOУ - координатная плоскость
 М1(х1, у1) ,
М1(х1, у1) ,  М2(х2, у2)
М2(х2, у2) 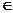 ХOУ
ХOУ
Найти: d= | M1M2 |
Ответ: 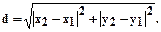
5.3.1.3. Деление отрезка в данном отношении
Дано: ХOУ - координатная плоскость
 М1(х1, у1),
М1(х1, у1),  М2(х2, у2)
М2(х2, у2) 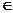 ХOУ
ХOУ
 М
М 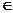 М1М2, |M1M| : |MM2| =
М1М2, |M1M| : |MM2| = 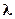
Найти:  М(х, у)
М(х, у)
Ответ: 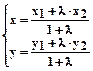

5.3.2. Косоугольная декартова система координат
 Y
Y

 y M(x, y)
y M(x, y)

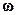
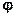
 О x X
О x X
XOY - косоугольная декартова система координат, 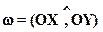 .
.
5.3.3. Полярная система координат
Полярная система координат на плоскости представляет собой положительное направление числовой прямой, которое называют полярной осью,
а начало координат - полюсом
 M(r,
M(r, 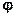 )
)
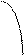 |
r
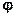
 полюс - О Р- полярная ось
полюс - О Р- полярная ось
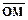 - радиус-вектор точки М,
- радиус-вектор точки М,
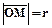 - полярный радиус точки М,
- полярный радиус точки М,
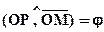 - полярный угол точки М.
- полярный угол точки М.
Каждой точке плоскости в этой системе координат соответствует упорядоченная пара чисел, из которых первое полярный радиус (r), а второе полярный угол ( 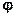 ).
).
Полярный угол всегда отсчитывается по направлению от полярной оси к радиусу-вектору данной точки. Удобно полагать, что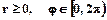 .
.
5.3.4. Связь между полярными и прямоугольными декартовыми координатами
Дано: XOY - прямоугольная декартова система координат
ОР || ОХ
ОР - полярная ось
 М(x, y)
М(x, y) 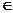 XOY,
XOY,  М(r ,
М(r , 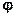 )
) 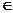 OP
OP
Найти: зависимости между (x, y) и (r , 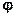 )
)
Ответ:
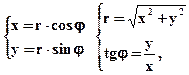
причем угол выбирается в соответствии со знаками хиу.
5.3.5. Параллельный перенос координатных осей
Дано: XOY - прямоугольная декартова система координат
 Q(x0 , y0)
Q(x0 , y0) 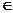 XOY
XOY
QXн || OX , QYн ||OY
Xн QYн - прямоугольная декартова система координат
 М(x, y)
М(x, y) 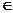 XOY,
XOY,  М(xн , yн)
М(xн , yн) 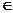 XнQYн
XнQYн
Найти: зависимости между (x, y) и (xн , yн)
Ответ: 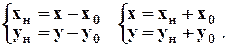
5.3.6. Поворот координатных осей
Дано: XOY - прямоугольная декартова система координат
Xн ОYн - прямоугольная декартова система координат
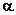 =(OХн
=(OХн  ОУн)
ОУн)
 М(x, y)
М(x, y) 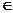 XOY,
XOY,  М(xн , yн)
М(xн , yн) 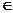 XнQYн
XнQYн
Найти: зависимости между (x, y) и (xн , yн)
Ответ: 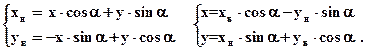
5.4. Прямоугольная декартова система координат в пространстве
 Z
Z
 zM3
zM3

 |
Дата добавления: 2015-08-26; просмотров: 1163;
