В дифференциальной форме. Ранее были получены уравнения Максвелла в интегральной форме

Ранее были получены уравнения Максвелла в интегральной форме. Основные четыре уравнения связывают характеристики электрического и магнитного полей в произвольной, но конечной области пространства, ограниченной замкнутой поверхностью 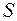или контуром :

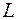, (36.1)

, (36.2)

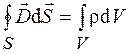, (36.3)

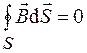. (36.4)

Для решения практических задач более удобными являются уравнения, которые связывают характеристики электромагнитного поля в бесконечно малой области пространства. Чтобы преобразовать уравнения Максвелла к дифференциальной форме, применим рассмотренные выше теоремы Остроградского–Гаусса и Стокса.

В соответствии с теоремой Остроградского–Гаусса потоки вектора индукции электрического и магнитного полей, которые входят в левые части уравнений (36.3) и (36.4), можно записать в виде 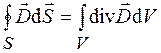и , где 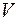– объем, ограниченный поверхностью 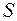. Тогда эти уравнения примут вид

,

.

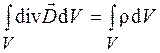Оба эти уравнения должны удовлетворяться для произвольного объема 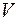. Для первого уравнения это может иметь место, если подынтегральные выражения в левой и правой частях равны, а для второго – подынтегральное выражение в левой части должно быть тождественно равно нулю. Таким образом, уравнения (36.3) и (36.4) принимают вид

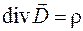, (36.5)

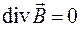. (36.6)

Полученные уравнения по-прежнему выражают теорему Гаусса для электрического и магнитного полей, но в дифференциальной форме. Уравнение (36.5) означает, что дивергенция вектора индукции 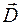электрического поля в произвольной точке пространства равна объемной плотности заряда в этой точке.В свою очередь, уравнение (36.6) означает, что дивергенция вектора индукции 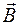магнитного поля в любой точке пространства равна нулю, т. е. магнитные заряды отсутствуют.

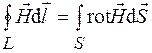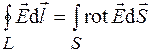В соответствии с теоремой Стокса левые части уравнений (36.1) и (36.2) можно записать в виде и , где 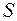– произвольная поверхность, ограниченная контуром 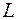. Тогда эти уравнения примут вид

,

.

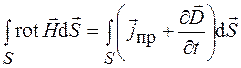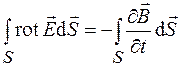Уравнения должны удовлетворяться для произвольной поверхности 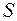, а это будет иметь место только в том случае, если подынтегральные выражения в левой и правой частях будут равны, т. е.

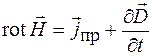, (36.7)

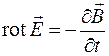, (36.8)

где 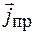– плотность тока проводимости; 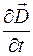– плотность тока смещения. Уравнение (36.7) выражает закон полного тока, а уравнение (36.8)– закон электромагнитной индукции в дифференциальной форме.Важно иметь в виду, что сделанные преобразования уравнений Максвелла не изменяют их физического смысла, а являются лишь иной математической формой записи этих уравнений.

Материальные уравнения и закон Ома в дифференциальной форме остаются без изменений, и таким образом полная система уравнений Максвелла в дифференциальной форме принимает вид

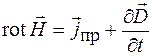, (36.9)

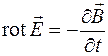, (36.10)

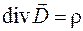, (36.11)

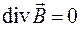, (36.12)

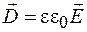, (36.13)

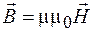, (36.14)

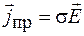. (36.15)