Волновое решение уравнений Максвелла

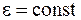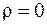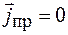Рассмотрим однородную среду ( ; ), в которой отсутствуют заряды и токи ( ; ). Тогда уравнения Максвелла примут вид

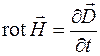, (38.1)

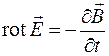, (38.2)

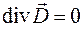, (38.3)

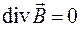. (38.4)

Применим операцию взятия ротора от левой и правой частей уравнения (38.2):

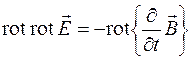. (38.5)

В соответствии с формулой (35.10) для левой части получим

.

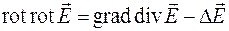Выражая напряженность электрического поля 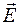через вектор индукции 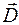, с учетом (38.3) последнее равенство можно записать в виде

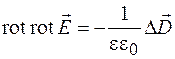. (38.6)

Правую часть уравнения (38.5), выразив индукцию магнитного поля через напряженность, с учетом (38.1) представим в виде

,

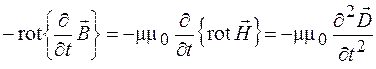и тогда уравнение (38.5) можно записать следующим образом:

. (38.7)

Применив операцию взятия ротора к левой и правой частям уравнения (38.1) и делая аналогичные преобразования, можно показать, что напряженность магнитного поля удовлетворяет уравнению

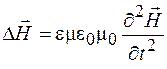. (38.8)

Сравнивая полученные уравнения (38.7), (38.8) с уравнением (35.9), можно сделать вывод: из уравнений Максвелла следует, что переменные электрическое и магнитное поля удовлетворяют волновому уравнению, а значит, могут распространяться в пространстве в виде электромагнитных волн. Они могут распространяться в среде, где отсутствуют свободные заряды и токи (в том числе и в вакууме). При этом скорость распространения электромагнитных волн

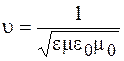(38.9)

и зависит от диэлектрических и магнитных свойств среды. Величина

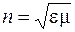(38.10)

называется показателем преломления среды. Показатель преломления – безразмерная величина. Для вакуума ( 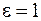и 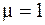) показатель преломления 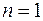и скорость распространения электромагнитных волн

.

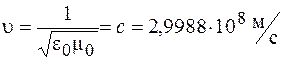Из (38.9) и (38.10) следует, что для произвольной среды с диэлектрической проницаемостью 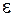и магнитной проницаемостью 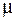скорость распространения электромагнитных волн меньше скорости света в вакууме:

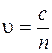. (38.11)

Из последнего равенства следует, что показатель преломления равен отношению скорости света в вакууме к скорости электромагнитных волн в данной среде.

Конкретный вид решения волновых уравнений (38.7), (38.8), т. е. форма электромагнитной волны, определяется начальными и граничными условиями.